FUNA-DB-käsikirja
Heidi Hellstrand a, Santeri Holopainen b, Johan Korhonen a, Pekka Räsänen b, Airi Hakkarainen c, Mikko-Jussi Laakso b, Anu Laine d ja Pirjo Aunio d
a Kasvatustieteiden ja hyvinvointialojen tiedekunta, Åbo Akademi, Vaasa
b Oppimisanalytiikan tutkimusinstituutti, Turun yliopisto, Turku
c Kasvatustieteiden ja psykologian tiedekunta, Jyväskylän yliopisto, Jyväskylä
d Kasvatustieteellinen tiedekunta, Helsingin yliopisto, Helsinki
Viittausohje: Hellstrand, H., Holopainen, S., Korhonen, J., Räsänen, P., Hakkarainen, A., Laakso, M.-J., Laine, A., & Aunio, P. (2025). FUNA-DB-käsikirja. Oppimisanalytiikan tutkimusinstituutti. https://www.oppimisanalytiikka.fi/ville/funa/manuals/funa-db-manual-fi/
Sisällys
Johdanto
FUNA-DB on matemaattisia perustaitoja mittaava seulontatesti perusopetuksen 3-9 luokille. FUNA tulee sanoista “Functional numeracy assessment” eli toiminnallisten laskutaitojen arviointi. Toiminnallisilla laskutaidoilla tarkoitetaan ymmärrystä ja kykyä käyttää perusmatemaattisia taitoja arjen eri tilanteissa. DB tulee sanoista “dyscalculia battery” ja viittaa siihen, että testin tarkoitus on tunnistaa ne lapset, joilla on hitautta tai ongelmia matemaattisten perustaitojen kehityksessä.
Tässä käsikirjassa kuvaillaan FUNA-DB-testiä ja sen tilastollisia analyysejä. Ensin luvussa 1 kuvaillaan FUNA-DB-testin tavoitetta ja sisältöä sekä analyysissä käytettävää aineistoa. Lukijan on syytä huomata, että osa analyyseistä perustuu Hakkaraisen et al. (2025) raporttiin, joten aineisto ei ole sama. Seuraavaksi luvussa 2 tarkastellaan testin luotettavuutta, mikä sisältää testin reliabiliteetin tarkastelun luvussa 2.1 ja testin validiteetin tarkastelun luvussa 2.2. Reliabiliteetin tutkiminen koostuu testin sisäisen johdonmukaisuuden (luku 2.1.1) sekä testi-uusintatesti-reliabiliteetin (luku 2.1.2) tutkimisesta. Validiteetin tutkiminen koostuu rakennevaliditeetin (luku 2.2.1), kulttuurien välisen validiteetin (luku 2.2.2), ryhmien erotteluvaliditeetin (luku 2.2.3), pitkittäisen mittausinvarianssin (luku 2.2.4), osatestien välisen yhtenevän validiteetin (luku 2.2.5) ja Lukukäsitteen rinnakkaisvaliditeetin (luku 2.2.6) tutkimisesta sekä yhtenevän validiteetin tutkimisesta RMAT-testin suhteen (luku 2.2.7).
Luvussa 3 tutkitaan luvussa 2.2.1 tarkastellun faktorirakenteen faktoripisteiden yhteyttä koulun kieleen, sukupuoleen sekä luokka-asteeseen. Lopuksi luvussa 4 on selitetty, miten opettaja voi tarkastella oman ryhmän tai oppilaan tuloksia ViLLE:n analytiikkanäkymässä. Käsikirjassa esitetyt analyysit on toteutettu R 4.3.0 ja Mplus 8.6 -ohjelmilla.
1 Testin ja aineiston kuvailu
Testin tarkoitus
FUNA-DB mittaa perusopetusikäisten (3–9-luokkalaisten) lasten matemaattisia perustaitoja. FUNA-DB:ssä keskitytään niihin perustaitoihin, jotka ovat osoittautuneet olevan yhteydessä myöhempään matemaattiseen oppimiseen, ja heikkous näissä perustaidoissa on hyvä tunnusmerkki sille, että lapsella voi olla matemaattinen oppimisvaikeus. Mikäli osaaminen näissä perustaidoissa on erittäin heikkoa, voi kyseessä olla dyskalkulia (Räsänen, 2012). FUNA-DB:n tarkoitus on löytää ne lapset, joilla on hitautta tai ongelmia matemaattisten perustaitojen kehityksessä. FUNA-DB ei näin ollen ole sidottu matematiikan oppimäärään eikä opetusmenetelmään.
FUNA-DB koostuu kuudesta osatestistä. Testissä on yhteensä 346 osiota, joista lapset tekevät vain osan tiettyjä osia koskevien aikarajoitteiden seurauksena. Testin avulla opettaja voi arvioida sitä, kuinka hyvin lapsi tai lapsiryhmä hallitsee matemaattiset perustaidot. Vertailemalla yhden lapsen saavutusta normiryhmän lasten tuloksiin voidaan todeta matemaattisten perustaitojen hallinnan taso suhteessa ikätasoon.
Perusopetusikäisten matemaattiset perustaidot
Matemaattisten perustaitojen, eli numeeristen perustaitojen, on todettu tutkimuksissa olevan pohja monimutkaisten matemaattisten taitojen oppimiselle (Butterworth, 2005; Jordan et al., 2009; Li et al., 2018). Varhaiset matemaattiset taidot, joiden kehitys alkaa jo päiväkodissa, ennustavat luotettavasti myöhemmin koulussa opittavia matemaattisia taitoja (Aunio & Niemivirta, 2010; Blume et al., 2021; Liu et al., 2025; Zhang et al., 2017). Tämän lisäksi tutkimukset ovat osoittaneet, että heikot matemaattiset (l. numeeriset) perustaidot ovat keskeistä niille lapsille ja nuorille, joilla on vaikea matemaattinen oppimisvaikeus (l. dyskalkulia) (De Smedt & Gilmore, 2011; Zhang et al., 2020).
Matemaattisten taitojen voidaan ajatella pohjautuvan kahdenlaiseen numeeriseen systeemiin. Ensinnäkin on olemassa symbolien käyttöön ja ymmärtämiseen perustuvat matemaattiset taidot, kuten esimerkiksi koulussa opittavat aritmeettiset taidot. Toiseksi ihmisillä on käytössään ei-symbolisten lukumäärien pohjalla toimiva lukumääräisyyden taju. Tällainen systeemi on myös löydetty eläimillä (Brannon & Terrace, 1998) ja jo pienillä lapsilla (Xu & Spelke, 2000). Yksilölliset erot tässä ei-symbolisessa lukumääräisyyden tajussa ovat yhteydessä koulussa opetettavaan numeeriseen symboliseen järjestelmään pohjautuvan matematiikan oppimiseen (Halberda, Mazzocco & Feigenson, 2008). Lukumääräisyyden tajua mitataan sekä numerosymbolien (numerosymbolinen lukumääräisyyden taju) että konkreettisten esineiden (ei-symbolinen lukumääräisyyden taju) avulla, esimerkiksi pisteiden lukumäärää vertailemalla, jolloin lasta pyydetään kertomaan kummassa joukossa on enemmän (De Smedt, Noël, Gilmore & Ansari, 2013). Lukumääräisyyden tajun on todettu kehittyvän varhaisvuosien aikana (Halberda & Feigenson, 2008), mutta etenkin ikäryhmässä 11-16 vuotta nähdään nopeaa kehitystä tässä taidossa (Halberda et al., 2012). Lukumääräisyyden taju on yhteydessä matemaattisiin taitoihin, mutta yksistään sen avulla ei voida tunnistaa vaikeaa matemaattista oppimisvaikeutta (De Smedt et al. 2013). FUNA-DB sisältää osatestejä, joissa lukumääriä esitellään sekä ei-numerosymboleilla (esim. pisteillä) että numerosymboleilla (numeroilla). FUNA-DB:ssä käsite lukukäsite viittaa lukumääräisuuden tajun osatesteihin.
Toinen suhteellisen itsenäinen matemaattinen perustaito on aritmeettinen sujuvuus (Petrill et al. 2012). Aritmeettisten taitojen sujumattomuus on selkeä tunnusmerkki matemaattisille oppimisvaikeuksille (Jordan & Hanich, 2003; Mazzocco, Devlin & McKenney, 2008). Sitä on käytetty jo pitkään osana terveydenhuollon käyttämiä kansainvälisiä diagnostiikkakriteereitä (ICD, DSM). Aritmeettinen sujuvuus on todettu olevan yhteydessä matemaattiseen osaamiseen koko kouluiän (Lee, Ng, & Bull, 2018; Price, Mazzocco, & Ansari, 2013; Vasilyeva, Lask & Shen, 2015; Xu et al. 2021). Aritmeettista sujuvuutta arvioidaan tehtävillä, joissa mitataan kuinka nopeasti lapsi, iästä riippuen, ratkaisee yksinkertaisia yhteen-, vähennys-, kerto- ja jakolaskutehtäviä. FUNA-DB sisältää osatestejä, jotka ovat aikarajoitteisia yhteen- ja vähennyslaskutehtäviä ja mittaavat aritmeettista sujuvuutta. FUNA-DB:ssä käsite laskusujuvuus viittaa näihin osatesteihin.
FUNA-DB:n kuvaus
Matemaattisten perustaitojen kuvauksessa on löydettävissä lasten välisiä eroja. Seulontatestit on suunniteltu löytämään sellaiset lapset, joilla on pulmia tutkittavalla oppimisen alueella. FUNA-DB:n päätarkoitus on löytää ne 3-9-luokkalaiset lapset, joilla epäillään olevan hitautta tai ongelmia matemaattisten perustaitojen kehityksessä. FUNA-DB:ssä mitataan matemaattisia perustaitoja kahdella eri taitoalueella: lukukäsite ja laskusujuvuus. Niitä arvioidaan kuudella osatestillä: lukujen vertailu, luvun ja määrän vastaavuus, lukusarjat, yhteenlaskut, vähennyslaskut ja laskutehtävät.
Osatesteistä lukujen vertailu ja luvun ja määrän vastaavuus mittaavat lukukäsitteen eli lukumääräisyyden hallintaa. Lukusarjat, yhteenlaskut, vähennyslaskut ja laskutehtävät mittaavat laskusujuvuutta. Testi rakentuu ajatukselle, että matemaattinen perustaito on kehittyvä taito. Vanhempien lasten oletetaan hallitsevan testin osatestejä paremmin kuin nuorten lasten, minkä vuoksi testin tuloksen tulkinnassa käytetään ikänormeja.
Lasten matemaattisten perustaitojen mittaaminen Suomessa
Suomessa lasten matemaattisten taitojen mittaaminen on osa psykologien ja opettajien työtä. Psykologien käytössä on ollut differentiaalipsykologiaan perustuvat David Wechslerin älykkyystestin laskutehtävät. Kouluikäisten lasten kanssa on käytetty Wechsler Intelligence Scale for Children- IV (WISC-IV) -testejä. Psykologien käytössä on ollut myös laskutehtäväosa testistä Lukilasse-2 (Häyrinen, Serenius-Sirve & Korkman, 2013), joka on tarkoitettu 1-6-luokkalaisten (6-13-vuotiaat) lasten taitojen arviointiin.
Opettajien käytössä ovat olleet MAKEKO (Ikäheimo et al., 1988; Ikäheimo et al., 2002) ja nykyisin MaKeKo 1-9 Kompassi -digikokeet (Ikäheimo, Putkonen & Voutilainen, n.d.), jotka mittaavat matematiikan keskeisen oppiaineksen hallintaa perusopetuksessa. Kymppikartoitusta (Ikäheimo, 2011) opettajat ovat voineet käyttää 2-6-luokkalaisten kanssa mittaamaan kymmenjärjestelmän ja mittayksikön muunnoksia. ALVA-ammattilaislaskennan kartoitusta (Ikäheimo, 2011) opettajat ovat voineet käyttää 8-10-luokkalaisten kanssa. Opettajien käytössä on myös ollut Salosen ja muiden (1994) kehittämän testipatteriston osa Diagnostiset testit 3: Motivaatio, metakognitio ja matematiikka mittaamaan koulutulokkaiden ja ensimmäisen luokan oppilaiden matemaattisten taitojen hallintaa. Taidon portaat -testistön matematiikkaosion avulla on voinut seurata ensiluokkalaisten taitojen kehitystä (Kananoja, 2001). Mavalkaa (Lampinen, Ikäheimo & Dräger, 2007) on käytetty arvioimaan matematiikan valmiuksia esiopetuksessa ja ensimmäisellä luokalla.
Matemaattisten oppimisvaikeuksien tunnistamisessa on ollut käytössä normeerattuja arviointivälineitä (kts. Mononen et al., 2017). Päiväkoti-ikäisten lasten matemaattisia suhde- ja laskemisen taitoja on voitu arvioida Lukukäsitetestillä (Van Luit et al., 2006). Esi- ja alkuopetusikäisten lasten matemaattista oppimisvaikeutta on voitu tunnistaa käyttämällä Lukimat-oppimisen arvioinnin välineitä (Lukimat.fi; Koponen et al., 2011), joissa keskitytään arvioimaan lukumääräisyyden tajua, matemaattisten suhteiden hallintaa, laskemisen taitoa sekä aritmeettisia perustaitoja. BANUCAn avulla on voitu tunnistaa oppimisvaikeudet luokilla 1-3, mittaamalla lukukäsitteen ja peruslaskutaidon osaamista (Räsänen, 2005). RMAT-laskutaidon testi on ollut käytössä ikäluokkien 3-6 kanssa, jolloin on keskitytty matemaattisten peruslaskutaitojen sujuvuuteen (Räsänen, 2004). MATTE-matematiikan sanallisten tehtävien ratkaisutaidon ja laskutaidon arviointia on käytetty 4-5-luokkalaisten kanssa (Kajamies et al., 2003). KTLT-laskutaidon testillä on arvioitu 7-9 -luokkalaisten peruslaskutaidon soveltamista (Räsänen & Leino, 2005).
Kuten edellisestä käy hyvin ilmi, Suomen perusopetukseen tarvitaan yksi kokoava, uuteen tutkimuskirjallisuuteen pohjautuva, normeerattu testi. Digitaalisuus tarjoaa mahdollisuuden lisätä matemaattisten oppimisvaikeuksien tunnistamisen luotettavuutta ja sujuvuutta.
FUNA-DB:n aiempi käytttö Suomessa
FUNA-DB:n kehittämistyö alkoi vuonna 2018 useiden suomalaisten yliopistojen tutkijoiden yhteistyönä. Ryhmässä on alusta asti ollut mukana asiantuntijoita koskien matemaattisten taitojen kehittymistä, oppimista ja oppimisvaikeuksia, oppimisen arviointia sekä oppimisanalytiikkaa. Ensimmäiset aineistot kerättiin vuonna 2020. Tämän käsikirjan pohja-aineisto on kerätty keväällä 2021. Vuoden 2020-2021 aineistosta on julkaistu tähän mennessä yksi kansainvälinen vertaisarvioitu artikkeli (Räsänen et al., 2021). Todisteet koskien FUNA-DB:n validiteetti- ja reliabiliteettiominaisuuksia on julkaistu kansainvälisissä vertaisarvioidussa artikkeleissa (Hellstrand et al., 2024; Hakkarainen et al., 2025).
FUNA-DB:n osatestien kuvaus
Tässä luvussa on testin kuuden osatestin kuvaus ja selvitys siitä, mitä kunkin osatestin on tarkoitus mitata.
1. Lukujen vertailu. Lukujen vertailussa näytölle ilmestyy kaksi yksinumeroista lukua. Lasta pyydetään valitsemaan mahdollisimman nopeasti ja tarkasti näistä kahdesta luvusta suurempi. Lapsi valitsee suuremman luvun painamalla näppäintä, joka on samalla puolella kuin suurempi luku. Tässä osatestissä on yhteensä 52 osiota.
2. Luvun ja määrän vastaavuus. Vastaavuuden osatestissä lasta pyydetään arvioimaan, onko näytölle ilmestyvä luku ja lukumäärä sama vai eri. Lasta pyydetään painamaan mahdollisimman nopeasti ja tarkasti oikeaa näppäintä. Toinen näppäin merkitsee, että luku on sama kuin pisteiden lukumäärä ja toinen näppäin merkitsee, että luku on eri kuin pisteiden lukumäärä. Näytöllä on numerosymboli vasemmalla puolella ja satunnaisesti järjestettyjä pisteitä oikealla puolella. Tässä osatestissä on yhteensä 42 osiota.
3. Lukusarjat. Lukusarjat-osatestissä lapselle näytetään neljä numeron lukusarja. Häntä pyydetään merkitsemään mikä luku tulee seuraavaksi, kun hän noudattaa sitä logiikkaa, millä lukusarja on tehty. Lapsi kirjoittaa seuraavan luvun numeronäppäimiä käyttäen. Lapsi tekee niin monta osiota kuin osaa ja ehtii kolmen minuutin aikana.
4. Yhteenlaskut (yksinumeroiset luvut). Lapselle esitetään yhteenlaskuja yksinumeroisilla luvuilla. Lapsi kirjoittaa vastauksen numeronäppäimiä käyttäen ja tekee niin monta osiota kuin osaa ja ehtii kahden minuutin aikana.
5. Vähennyslaskut (yksinumeroiset luvut). Lapselle esitetään vähennyslaskuja yksinumeroisilla luvuilla. Lapsi kirjoittaa vastauksen numeronäppäimiä käyttäen ja tekee niin monta osiota kuin osaa ja ehtii kahden minuutin aikana.
6. Laskutehtävät (moninumeroiset luvut). Lasta pyydetään ratkaisemaan yhteen- ja vähennyslaskutehtäviä, joissa käytetään kaksi-, kolme- ja neljänumeroisia lukuja. Yhteen- ja vähennyslaskut tulevat sekajärjestyksessä. Lapsi tekee niin monta osiota kuin osaa ja ehtii kolmen minuutin aikana.
Testin osiot
Testin osatestit perustuvat tämänhetkiseen kansainväliseen tutkimukseen, jossa on selvitetty matemaattisten taitojen kehitystä ja oppimisvaikeuksien tunnusmerkkejä. Lapsen tekemät osiot osatesteissä ovat peräisin suuremmasta osioiden joukosta (osiopankista). Osiot esitetään lapselle visuaalisesti tietokoneen avulla ja lapsi käyttää tietokoneen näppäimiä osioihin vastatessa. Lapsi lukee ohjeen näytöltä. Jokainen osio pisteytetään oikeaksi (1 pistettä) tai vääräksi (0 pistettä).
Ennen jokaista osatestiä edeltää muutama harjoitustehtävä, joissa lapsi voi harjoitella osatestin tekemistä ja ymmärtää, mitä häneltä kysytään ja miten vastata. Harjoitustehtävien kohdalla opettaja voi myös opastaa lapsia.
Käyttäjävaatimukset
Testi on tarkoitettu (erityis)opetuksen ammattilaisten ja psykologien työkaluksi. Testaamisessa ja tulosten tulkinnassa on oleellista seurata tässä käsikirjassa annettuja ohjeita. Testaajan kannattaa perehtyä ohjeisiin huolellisesti ennen lasten taitojen mittaamista.
Testin sovellusalue
FUNA-DB on suunniteltu käytettäväksi 3-9-luokkalaisten (9-16-vuotiaiden) lasten (erityis)pedagogisessa arvioinnissa määrittämään lapsen matemaattisten perustaitojen osaamista. Testin perustehtävä on tunnistaa se joukko lapsia, joilla on heikkoutta matemaattisissa perustaidoissa.
1.1 Aineisto
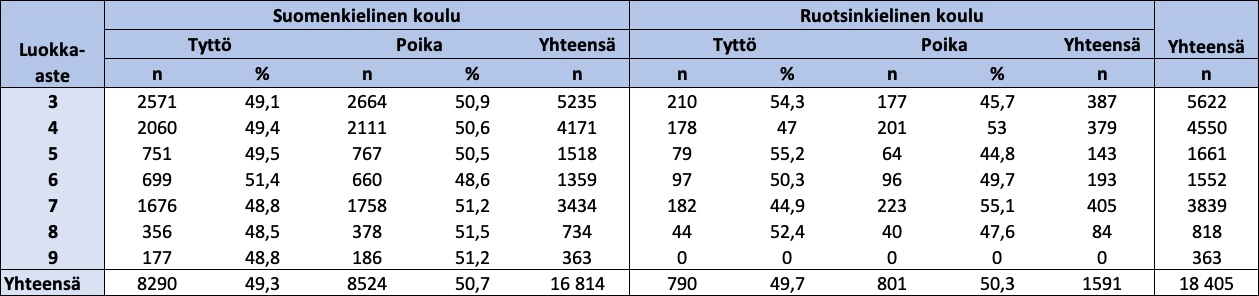
FUNA-DB-testin aineisto koostuu 18 409 3–9-luokkalaisesta lapsesta suomen- ja ruotsinkielisistä kouluista eri puolilta Suomea. Analyyseissä käytettävän aineiston koko on N = 18 405, sillä neljällä lapsella on puuttuva arvo jokaisen relevantin muuttujan kohdalla (eli jokaisen pistemäärämuuttujan kohdalla, jotka määritellään myöhemmin) aineiston siivouksen jälkeen. Suomenkielistä koulua käyviä lapsia oli yhteensä 16 814 (91,4 %) ja ruotsinkielistä koulua käyviä lapsia 1 591 (8,6 %). Tyttöjä oli yhteensä 9 080 (49,3 %) ja poikia 9 325 (50,7 %). 3-luokkalaisia oli yhteensä 5 622 (30,5 %), 4-luokkalaisia 4 550 (24,7 %), 5-luokkalaisia 1 661 (9,0 %), 6-luokkalaisia 1 552 (8,4 %), 7-luokkalaisia 3 839 (20,9 %), 8-luokkalaisia 818 (4,4 %) ja 9-luokkalaisia 363 (2,0 %). Taulukossa 1 näkyy koko aineiston lasten määrä jaoteltuna luokka-asteen, sukupuolen ja koulun kielen mukaan.
Taulukko 1
Aineiston lasten määrä jaoteltuna luokka-asteen, sukupuolen ja koulun kielen mukaan
1.2 Testi ja sen kuvailevat tunnusluvut
FUNA-DB-testi koostuu kahdesta kokonaisuudesta ja yhteensä kuudesta osatestistä. Lukukäsite sisältää osatestit Lukujen vertailu (F1.1) ja Luvun ja määrän vastaavuus (F1.2). Laskusujuvuus sisältää osatestit Lukusarjat (F2.1), Yhteenlaskuja (F3.1), Vähennyslaskuja (F3.2) ja Laskutehtäviä (F3.3). Kullekin lapselle laskettiin osatestikohtaiset pisteet. Osatestien F1.1 ja F1.2 pisteet ovat tehokkuusindeksejä (l. oikeiden vastausten reaktioajan mediaani jaettuna oikeiden vastausten prosenttiosuudella) ja osatestien F2.1, F3.1, F3.2 ja F3.3 pisteet ovat summapisteitä (l. oikeiden vastausten lukumäärä osatestikohtaisen aikamääreen sisällä). Taulukossa 2 näkyy kunkin osatestin nimi, selite, käytettävä pistemäärä, aikaraja ja osioiden lukumäärä.
Taulukko 2
Tietoa FUNA-DB:n osatesteistä
Ennen osatestien pisteiden kuvailevien tunnuslukujen laskemista ja jatkoanalyysejä aineistoa siivottiin eli joitakin arvoja poistettiin aineistosta, kun tietyt ehdot täyttyivät. Lukukäsite-kokonaisuuden osatestien F1.1 ja F1.2 kohdalla aineistoa siivottiin seuraavasti: ensin poistettiin ne vastausajat, jotka olivat yli kolmen keskihajonnan verran suurempia kuin keskiarvo. Samoin poistettiin ne vastausajat, jotka olivat alle 200 millisekuntia, sillä niitä pidettiin epärealistisina, liian lyhyinä, vastausaikoina. Osatestin F1.1 kohdalla poistettiin lisäksi ne osiot, joissa oli joko vasemmalla tai oikealla puolella numero 1 tai 9. Toisessa vaiheessa tehtiin oletus, että osatestien F1.1 ja F1.2 kaikki vastaukset olivat arvauksia ja oikean vastauksen binomitodennäköisyys oli 0,65. Täten aineistosta poistettiin ne tapaukset, joiden oikeiden vastausten lukumäärä oli alle 65 % maksimista (F1.1: 0,65⨉52=34 ja F1.2: 0,65⨉42=27). Laskusujuvuus-kokonaisuuden osatesteissä F2.1-F3.3 oli avoin vastauskenttä, joten niiden kohdalla aineiston siivouksessa käytettiin erilaista menetelmää: tapaukset, joilla oli vähemmän kuin kaksi oikeaa vastausta, poistettiin aineistosta.
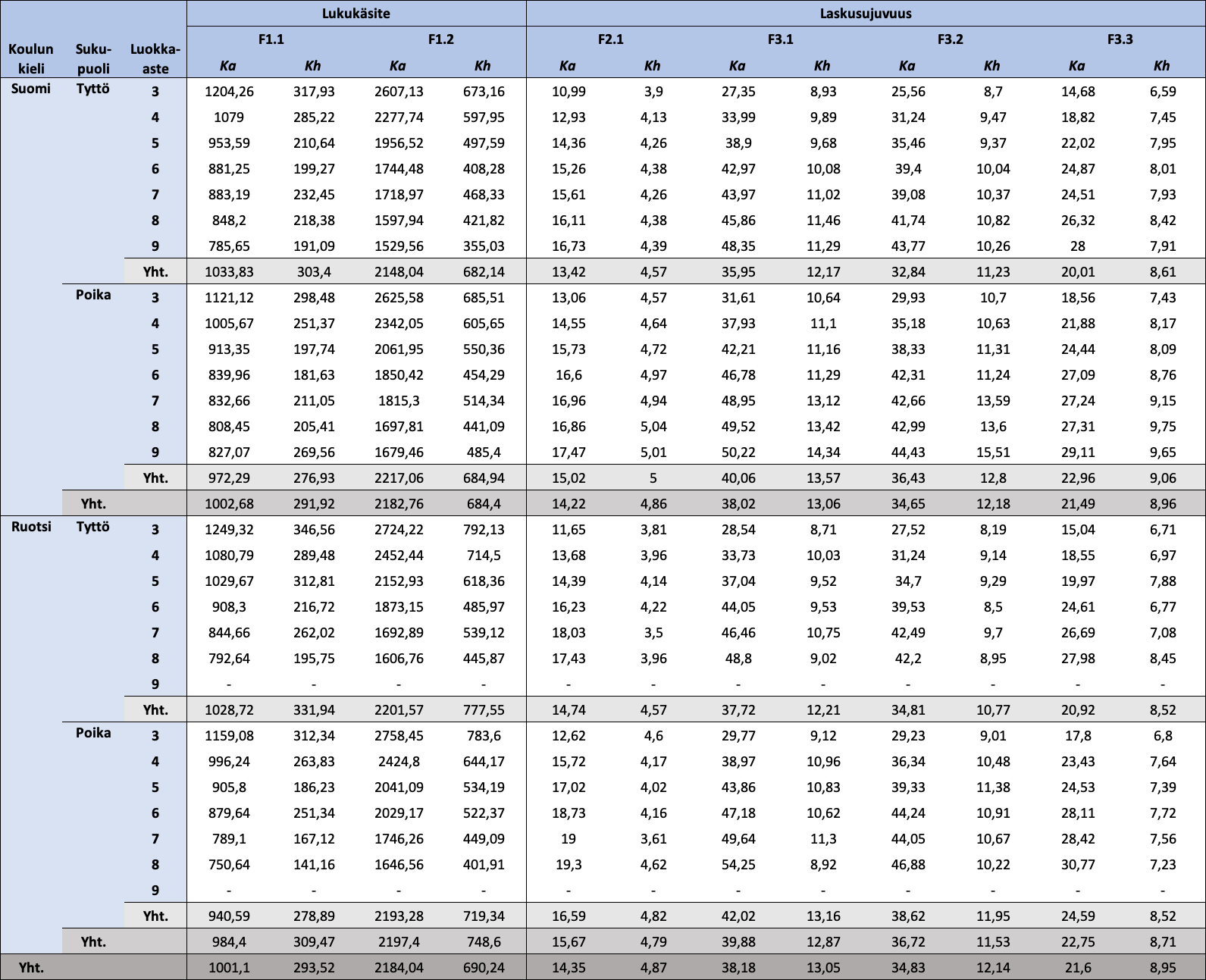
Koulun kielen, sukupuolen ja luokka-asteen mukaan jaotellut osatestikohtaiset keskimääräiset raakapisteet ja raakapisteiden keskihajonnat näkyvät taulukossa 3, jonka kohdalla on syytä huomioida, että tehokkuusindeksien arvot osatesteille F1.1 ja F1.2 ovat sitä parempia, mitä pienempiä ne ovat, ja summapisteiden arvot osatesteille F2.1-F3.3 ovat sitä parempia, mitä suurempia ne ovat. On syytä huomata myös se, että osatestien pisteiden arvojoukot ovat hyvin erilaisia, mikä johtuu pisteiden erilaisista laskutavoista ja osatestien erilaisista rakenteista (aikarajat ja osioiden lukumäärät eivät ole samansuuruisia). Raakapisteiden arvojoukot ([minimi, maksimi]) ovat F1.1: [459,15; 3452,93], F1.2: [415,50; 8102,93], F2.1: [2, 35], F3.1: [2, 80], F3.2: [2, 80] ja F3.3: [2, 57]. Täten tunnuslukuja ei voi verrata suoraan keskenään (esimerkiksi osatestin F1.1 keskiarvo on 1001,10; mutta osatestin F2.1 keskiarvo on 14,35). Sen sijaan yksittäisen osatestin raakapisteitä voi verrata kieliryhmien, sukupuolten ja luokka-asteiden kesken.
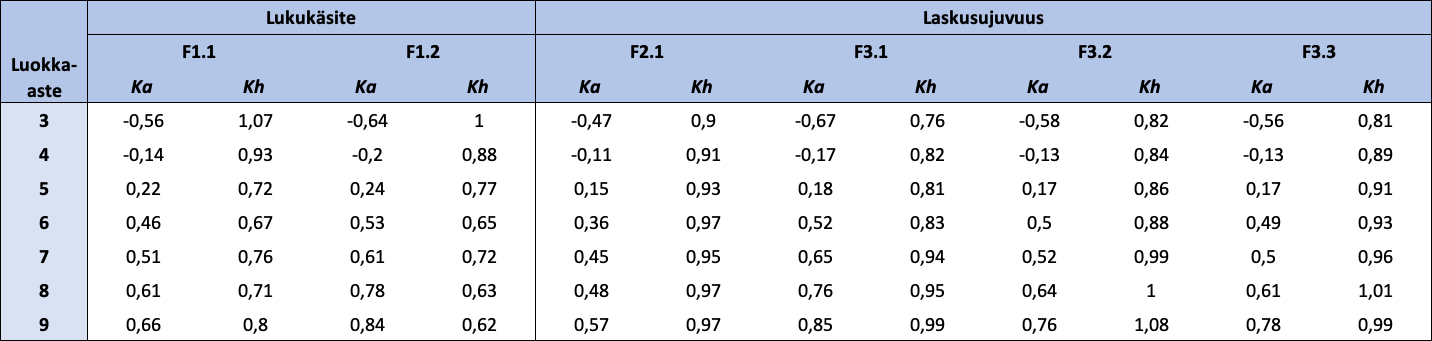
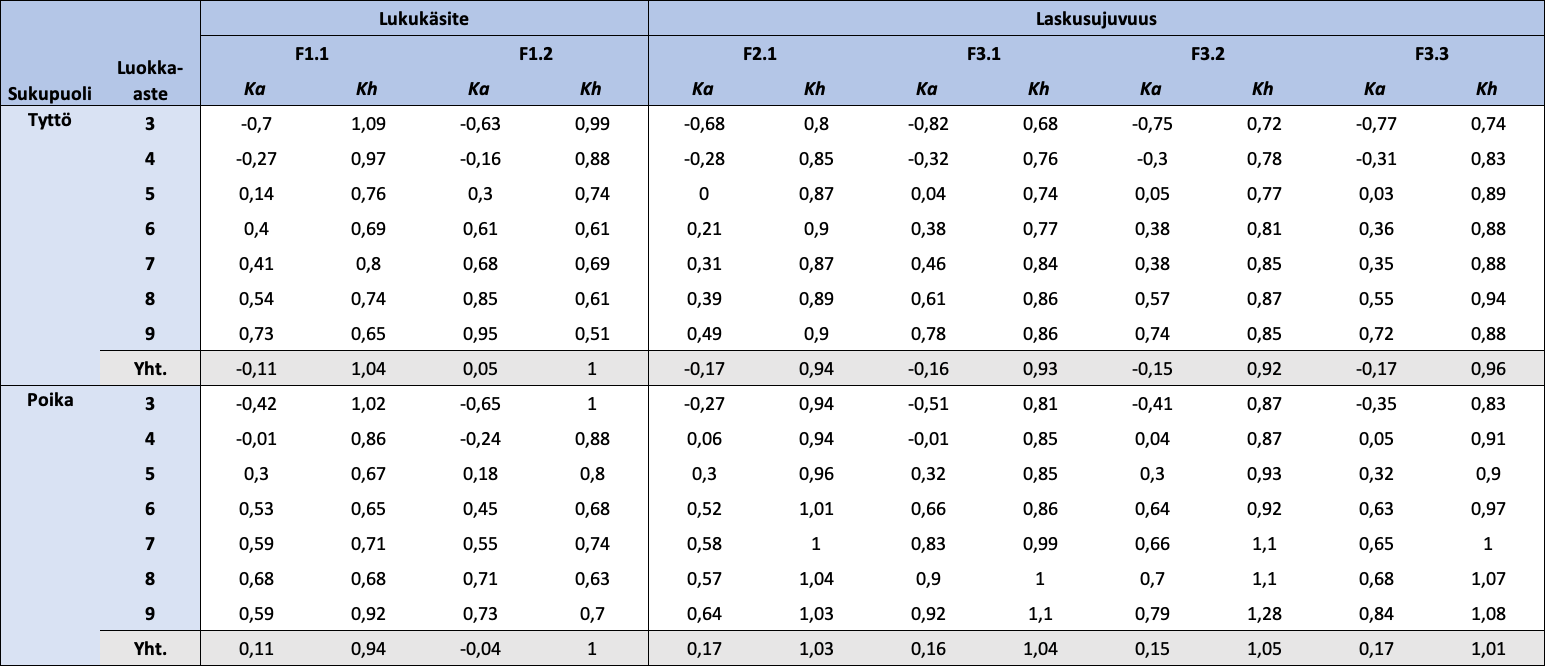
Taulukoissa 4-6 näkyvät osatestien standardoitujen pisteiden keskiarvot ja keskihajonnat. Standardointi tarkoittaa sitä, että jokaisen osatestin pistemäärän keskiarvo on 0 ja keskihajonta 1. Lukukäsitteen osatestien F1.1 ja F1.2 pisteet ovat myös käännettyjä, jolloin päättely on samanlainen kuin Laskusujuvuuden osatestien F2.1-F3.3 tapauksessa: mitä suurempi lapsen pistemäärä osatesteissä F1.1 ja F1.2 on, sitä paremmin lapsi on pärjännyt näissä osatesteissä. Taulukossa 4 keskiarvot ja keskihajonnat on jaoteltu pelkästään luokka-asteittain, taulukossa 5 sukupuolittain sekä luokka-asteittain ja taulukossa 6 kieliryhmittäin sekä luokka-asteittain. Liitteessä 1 on ylimääräisiä/täydentäviä taulukoita osatestien raakapisteiden sekä standardoitujen pisteiden kuvailevista tunnusluvuista.
Taulukko 3
Koulun kielen, sukupuolen ja luokka-asteen mukaan jaotellut FUNA-DB:n osatestien raakapisteiden kuvailevat tunnusluvut
Huom. N = 18405. Ka = keskiarvo; Kh = keskihajonta. Mitä vähemmän pisteitä Lukukäsitteen osatesteistä, sitä parempi tulos, ja mitä enemmän pisteitä Laskusujuvuuden osatesteistä, sitä parempi tulos. Osatestien pisteiden arvojoukot ([minimi, maksimi]) ovat F1.1: [459,15; 3452,93], F1.2: [415,50; 8102,93], F2.1: [2, 35], F3.1: [2, 80], F3.2: [2, 80] ja F3.3: [2, 57].
Taulukko 4
Luokka-asteen mukaan jaotellut FUNA-DB:n osatestien standardoitujen pisteiden kuvailevat tunnusluvut
Huom. N = 18 405. Ka = keskiarvo; Kh = keskihajonta. Lukukäsitteen osatestien pisteet ovat standardoinnin lisäksi käännettyjä.
Taulukko 5
Sukupuolen ja luokka-asteen mukaan jaotellut FUNA-DB:n osatestien standardoitujen pisteiden kuvailevat tunnusluvut
Huom. N = 18 405. Ka = keskiarvo; Kh = keskihajonta. Lukukäsitteen osatestien pisteet ovat standardoinnin lisäksi käännettyjä.
Taulukko 6
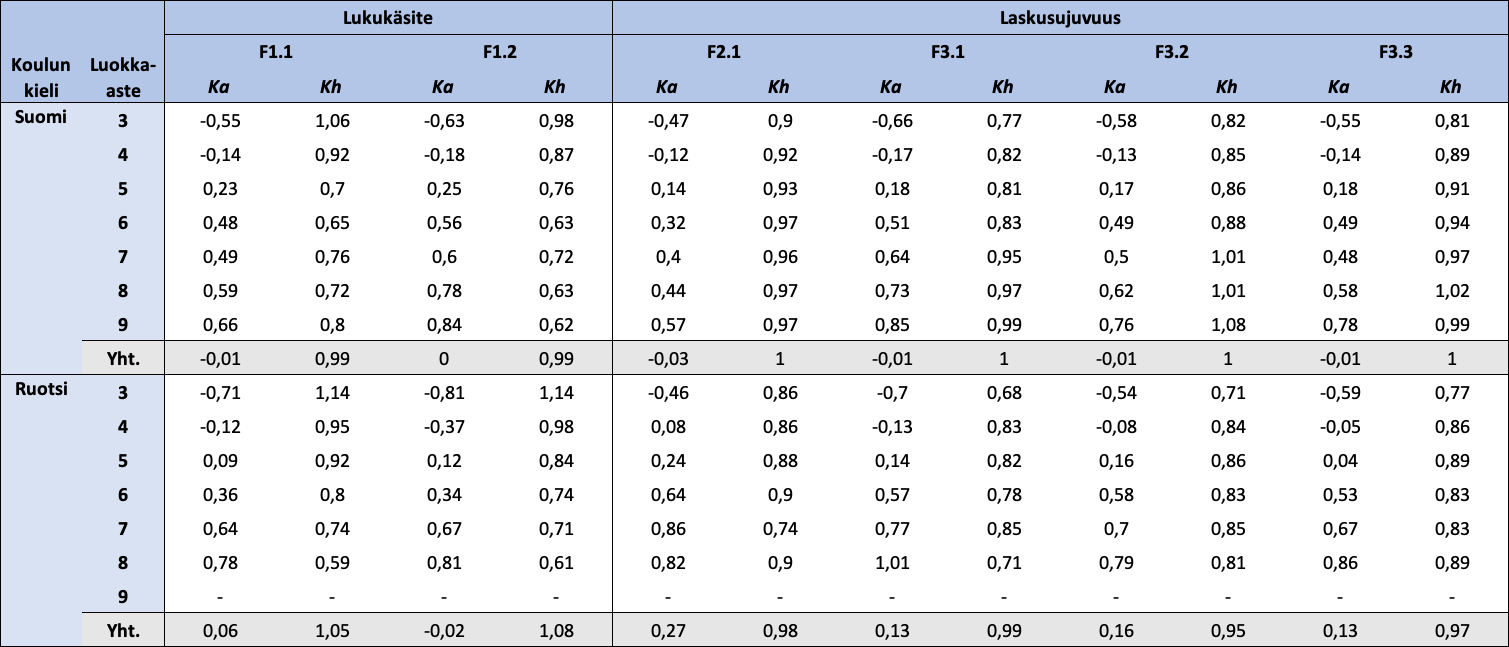
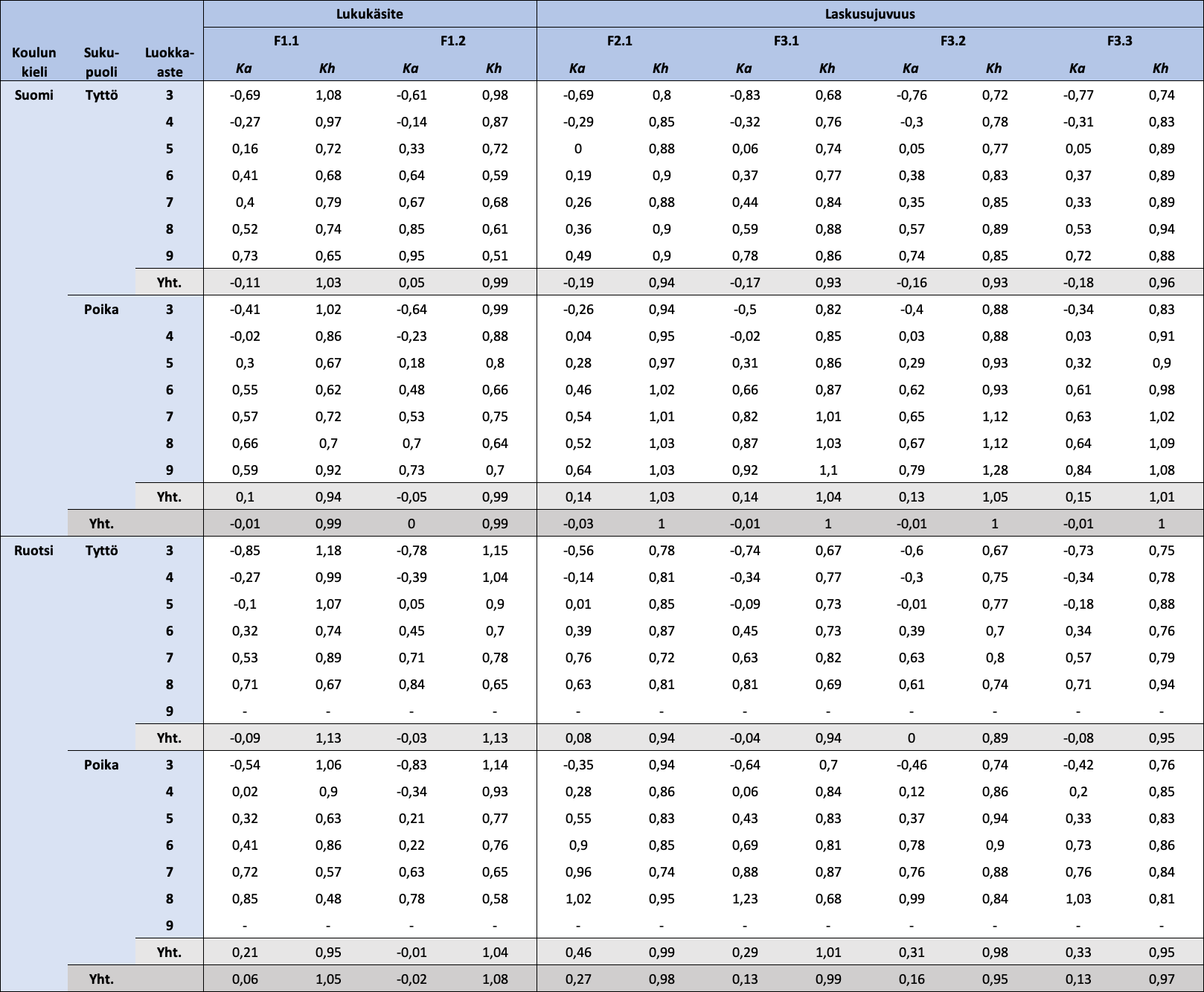
Koulun kielen ja luokka-asteen mukaan jaotellut FUNA-DB:n osatestien standardoitujen pisteiden kuvailevat tunnusluvut
Huom. N = 18 405. Ka = keskiarvo; Kh = keskihajonta. Lukukäsitteen osatestien pisteet ovat standardoinnin lisäksi käännettyjä.
2 Testin luotettavuus
Testin luotettavuuden arviointi koostuu testin reliabiliteetti- ja validiteettiominaisuuksien tarkastelusta. Suurin osa analyyseistä perustuu yllä kuvailtuun 18 405 lapsen aineistoon, jota analysoitiin myös Hellstrandin et al. (2024) artikkelissa. Osa analyyseistä, joita ei voitu toteuttaa pelkästään yhdellä aineistolla, perustuvat Hakkaraisen et al. (2025) tekemiin analyyseihin. Hakkarainen et al. (2025) tutkivat FUNA-DB:n testi-uusintatesti-reliabiliteettia, pitkittäistä mittausinvarianssia sekä yhtenevää validiteettia. Heidän aineistonsa koostui 358 lapsesta luokilla 3 (N = 93), 5 (N = 131) ja 7 (N = 134), joista 165 oli poikia ja 193 tyttöjä. Testi-uusintatesti-reliabiliteetin sekä pitkittäisen mittausinvarianssin tutkimista varten lapset osallistuivat tutkimukseen kahdessa eri aikapisteessä 2–4 viikon välillä vuonna 2021.
2.1 Reliabiliteetti ja mittavirheet
2.1.1 Testin sisäinen johdonmukaisuus ja mittavirheet
FUNA-DB:n sisäisen johdonmukaisuuden (engl. internal consistency) reliabiliteettia arvioidaan laskemalla Spearmanin-Brownin sekä Guttmanin (Guttmanin λ₄) reliabiliteettikertoimet. Spearmanin-Brownin kerrointa laskettaessa FUNA-DB:n kukin osatesti jaetaan satunnaisesti kahteen puolikkaaseen. Tämän jälkeen lasketaan puolikkaiden välinen korrelaatio, jonka avulla pystytään laskemaan osatestikohtaisten reliabiliteettikertoimien arvot (puolitusmenetelmä; engl. split-half method). Guttmanin kertoimet kullekin osatestille lasketaan R-ohjelman psych-paketin splitHalf-funktion avulla, joka muodostaa mahdollisimman suuren määrän mahdollisia puolituksia kyseessä olevalle osatestille ja valitsee puolitusten avulla lasketuista Guttmanin reliabiliteettikertoimen arvoista suurimman (Revelle, 2021). Sekä Spearmanin-Brownin että Guttmanin reliabiliteettikertoimen arvon pitäisi olla yli 0,7; jotta kyseessä olevan osatestin voitaisiin päätellä olevan sisäisesti johdonmukainen (Hays & Revicki, 2005).
Tämän jälkeen Spearmanin-Brownin reliabiliteettikertoimien avulla kullekin osatestille lasketaan koko aineiston sekä eri luokka-asteiden mittavirheiden (engl. standard error of measurement, SEM) estimaatit. SEM kertoo kyseessä olevan osatestin keskimääräisen mittausvirheen suuruuden eli sen, kuinka paljon lapsen tai ryhmän havaittu pistemäärä poikkeaa keskimääräisesti aidosta pistemäärästä (pistemäärä, jonka lapsi tai ryhmä saisi, jos testissä ei olisi yhtään mittausvirhettä) (Musselwhite & Wesolowski, 2018). SEM-estimaatteja käyttäen lasketaan vielä koko aineiston ja eri luokka-asteiden aitojen pistemäärien 95 %:n luottamusvälit (väli, joka sisältää aidon pistemäärän 95 % tapauksista aineistonkeruuta toistettaessa).
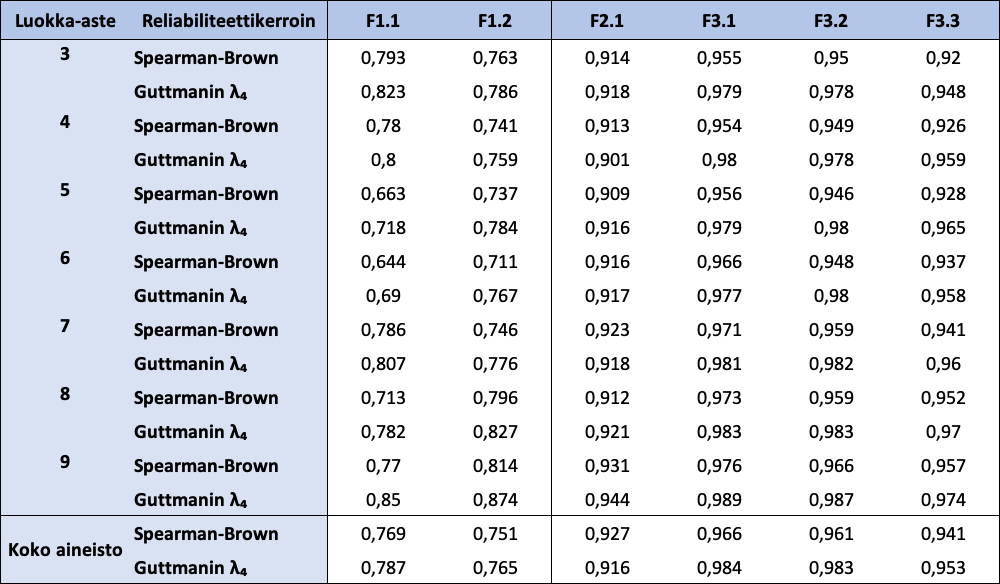
FUNA-DB:n osatestien reliabiliteettikertoimet esitetään taulukossa 7. Reliabiliteettikertoimet ovat korkeita sekä koko aineistolle että luokka-asteittain lukuun ottamatta luokka-asteen 5 Spearmanin-Brownin reliabiliteettikertoimen arvoa sekä luokka-asteen 6 molempien reliabiliteettikertoimien arvoja osatestille F1.1, jotka ovat alle 0,7. Koko aineiston ja eri luokka-asteiden mittavirheiden estimaatit ja osatestien aitojen pisteiden 95 %:n luottamusvälit ovat esillä taulukossa 8. Osatestin F1.1 mittavirheiden estimaatit vaihtelevat välillä 103,04 – 142,17; osatestin F1.2 välillä 186,28 – 344,24; osatestin F2.1 välillä 1,24 – 1,40; osatestin F3.1 välillä 2,00 – 2,40; osatestin F3.2 välillä 2,22 – 2,46 ja osatestin F3.3 välillä 1,83 – 2,17. Mitä pienempi mittavirheen estimaatin arvo on, sitä tarkempi havaittu pistemäärä on (ottaen huomioon havaitun pistemäärän suuruuden).
Taulukko 7
FUNA-DB:n osatestien reliabiliteettikertoimet koko aineistolle sekä luokka-asteittain
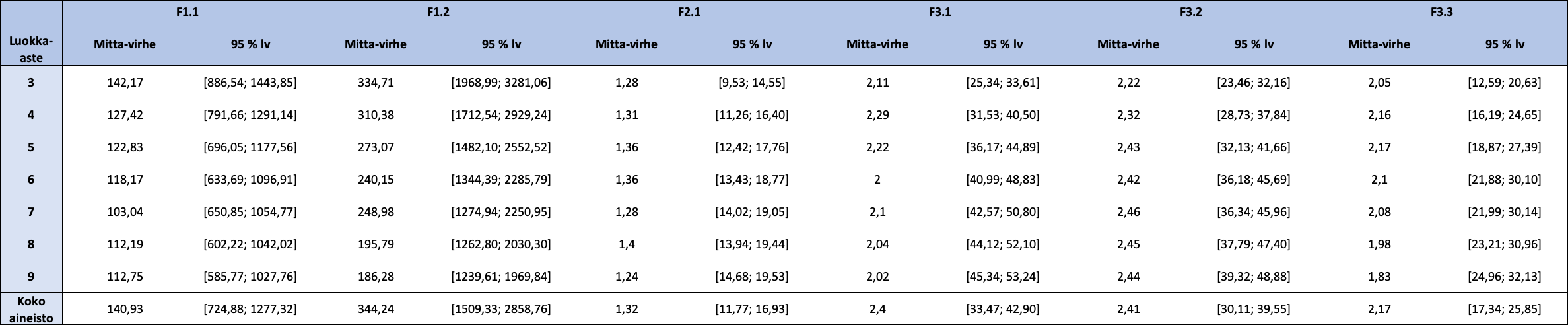
Taulukko 8
FUNA-DB:n osatestien mittavirheiden estimaatit ja aitojen pisteiden 95 prosentin luottamusvälit koko aineistolle sekä luokka-asteittain
Huom. 95 % lv = 95 prosentin luottamusväli.
2.1.2 Testi-uusintatesti-reliabiliteetti
FUNA-DB:n testi-uusintatesti-reliabiliteettitarkastelut tehtiin Hakkaraisen et al. (2025) raportissa. Sekä Lukukäsite- (r = 0,84) että Laskusujuvuus-faktorilla (r = 0,90) oli korkea korrelaatio mittauspisteiden välillä, minkä perusteella FUNA-DB:n testi-uusintatesti-reliabiliteetti oli erinomainen. Myös yksittäisten osatestien korrelaatiot aikapisteiden välillä olivat korkeita. Lukukäsite-faktorissa havaittiin pieni jäännevaikutus (engl. carry-over effect), sillä lapset pärjäsivät keskimäärin hieman paremmin toisella kerralla kuin ensimmäisellä. Laskusujuvuus-faktorissa ei havaittu jäännevaikutusta (Hakkarainen et al., 2025).
2.2 Validiteetti
Testin rakennevaliditeettia tutkitaan tarkastelemalla yhden ja kahden faktorin rakenteita konfirmatorisella faktorianalyysillä. Kulttuurien välistä validiteettia (engl. cross-cultural validity) ja ryhmien erotteluvaliditeettia (engl. known-group validity) tutkitaan tarkastelemalla rakennevaliditeettia erikseen suomen- ja ruotsinkielisten koulujen lapsille (kulttuurien välinen validiteetti), tytöille ja pojille sekä eri luokka-asteiden lapsille (ryhmien erotteluvaliditeetti). Tämän lisäksi tutkitaan, toteutuuko mittausinvarianssi, eli onko testi muuttumaton kieliryhmien, sukupuolten ja luokka-asteiden yli. Osatestien välinen yhtenevä validiteetti (engl. convergent validity) nähdään laskemalla osatestien väliset korrelaatiot. Lukukäsitteen rinnakkaisvaliditeettia (engl. concurrent validity) suhteessa Laskusujuvuuteen tutkitaan ROC-analyysiä (engl. receiver operating characteristic) hyödyntäen. Viimeinen validiteettia käsittelevä luku koskee FUNA-DB:n yhtenevää validiteettia RMAT-testin suhteen ja perustuu Hakkaraisen et al. (2025) raporttiin, jossa he laskivat FUNA-DB:n faktorien ja RMAT-testin välisiä korrelaatioita.
2.2.1 Rakennevaliditeetti (structural validity)
FUNA-DB-testin rakennevaliditeetti evaluoidaan konfirmatorisella faktorianalyysillä (engl. confirmatory factor analysis, CFA). Aiemman tutkimuksen perusteella muodostetaan kaksi faktoria (De Smedt, Noël, Gilmore & Ansari, 2013; Mazzocco, Devlin & McKenney, 2008). Lukukäsite-faktori latautuu osatesteistä F1.1 ja F1.2 laskettuihin tehokkuusindekseihin ja Laskusujuvuus-faktori latautuu osatesteistä F2.1, F3.1, F3.2 ja F3.3 laskettuihin summapisteisiin. Tässä on jälleen syytä huomioida, että tehokkuusindeksien ja summapisteiden tulkinta on erilainen: mitä pienemmät tehokkuusindeksien arvot ovat, sitä paremmin lapsi suoriutui osatesteistä F1.1 ja F1.2, mutta mitä suuremmat summapisteet ovat, sitä paremmin lapsi suoriutui osatesteistä F2.1-F3.3. Kyseiset tehokkuusindeksit ja kokonaispisteet ovat tässä analyysissä indikaattorimuuttujia ja niitä käsitellään jatkuvina, joten CFA-analyysissä estimointimenetelmänä käytetään suurimman uskottavuuden menetelmää, erityisesti täyden informaation suurimman uskottavuuden menetelmää, koska se käyttää kaikkea käytettävissä olevaa aineistoa mallin sovituksessa (Arbuckle, 1996). Kahden faktorin mallin vertailumalliksi otetaan yhden faktorin malli, jossa yksi faktori (FUNADB) kuvastaa numeerisia perustaitoja.
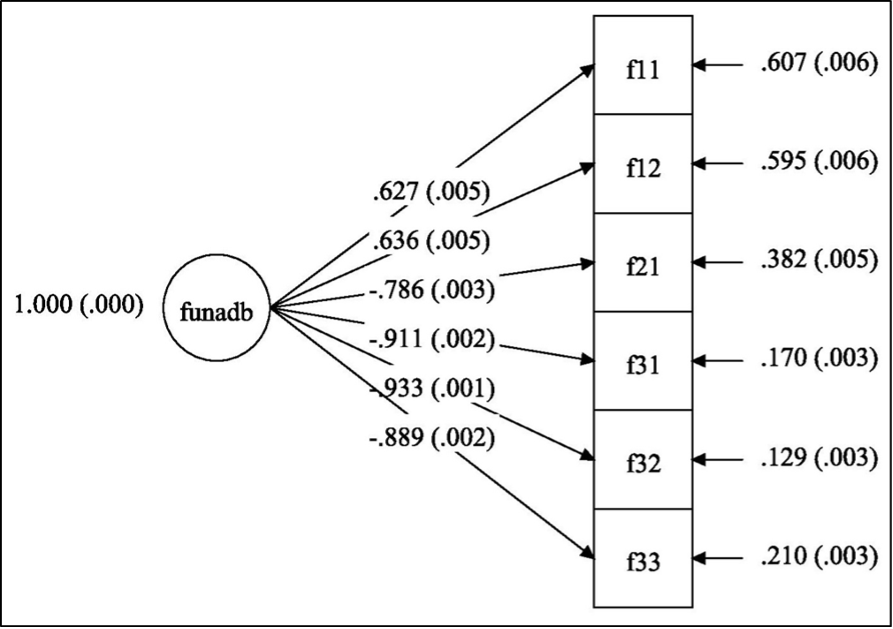
Kuva 1
FUNA-DB:n konfirmatorinen faktorianalyysi: yhden faktorin mallin polkukuvio
Huom. N = 18 405. FUNADB = numeeristen perustaitojen faktori. Estimointimenetelmänä käytettiin täyden informaation suurimman uskottavuuden menetelmää (engl. full information maximum likelihood, FIML). Parametriestimaatit ovat standardoituja ja latentin faktorin varianssi on asetettu ykköseen. Keskivirheet ovat suluissa parametriestimaattien vieressä. Kaikki parametriestimaatit erosivat tilastollisesti merkitsevästi nollasta. Osatestien F2.1-F3.3 negatiiviset faktorilataukset johtuvat osatesteistä F1.1-F1.2 ja osatesteistä F2.1-F3.3 laskettujen pisteiden tulkinnallisesta erosta.
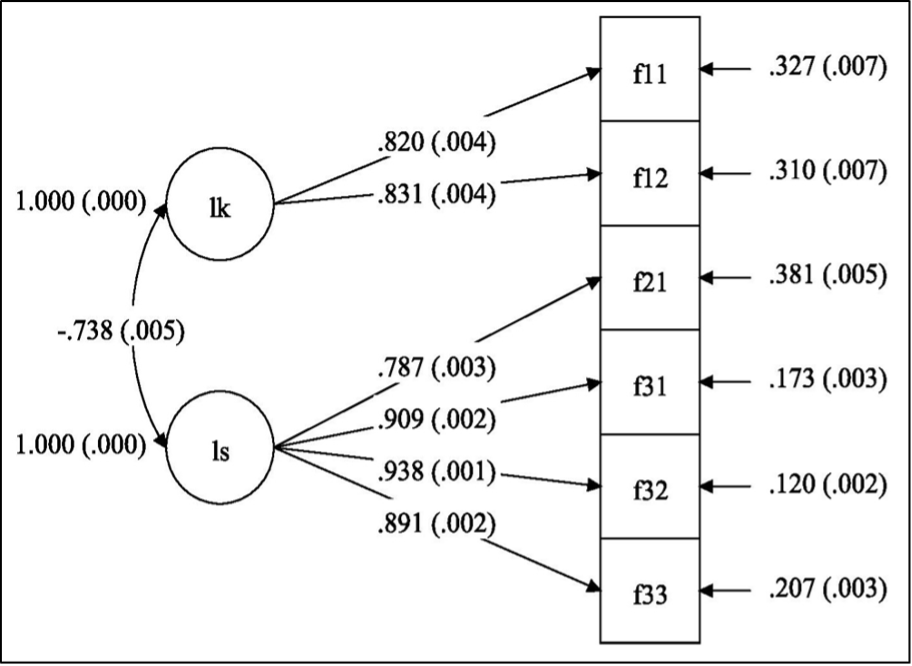
Yhden faktorin mallissa standardoidut faktorilataukset osatestien F2.1-F3.3 summapisteisiin ovat negatiivisia, mikä johtuu aiemmin mainitusta tehokkuusindeksien ja summapisteiden tulkinnallisesta erosta (Kuva 1). Sama ilmiö näkyy myös kahden faktorin mallissa, jossa faktorien Lukukäsite ja Laskusujuvuus välinen estimoitu korrelaatio on negatiivinen (Kuva 2). Kahden faktorin mallissa kaikki faktorilataukset ovat melko korkeita (> 0,7). CFA-analyysin perusteella kyseisen mallin jokainen faktorilataus eroaa tilastollisesti merkitsevästi nollasta merkitsevyystasolla 0,001.
Mallin sopivuuden indikaattoreina käytetään sopivuusindeksejä Root Mean Square Error of Approximation (RMSEA), Comparative Fit Index (CFI) ja Tucker-Lewis Index (TLI). RMSEA-estimaatin arvot, jotka ovat pienempiä kuin 0,05 ja 0,08; indikoivat mallin läheisestä ja kohtuullisesta sopivuudesta aineistoon. Vastaavasti CFI- ja TLI-indeksien arvot, jotka ovat suurempia kuin 0,9 ja 0,95 indikoivat mallin hyväksyttävästä ja erinomaisesta sopivuudesta aineistoon. (Marsh, Hau, & Wen, 2004) Näiden lisäksi raportoidaan Khiin neliön (χ²) testin tulokset, koska RMSEA-, CFI- ja TLI-indeksien arvot riippuvat kyseisen testisuureen arvosta. Kun tarkastellaan yhden ja kahden faktorin mallien sopivuusindeksejä (Taulukko 9), huomataan, että yhden faktorin mallin sopivuus aineistoon on erittäin huono. χ²-testin mukaan kyseinen malli eroaa tilastollisesti merkitsevästi ideaalista mallista: χ²(9) = 5920,80; p < 0,001. Tämä tulos oli odotettavissa erittäin suuren otoskoon vuoksi. RMSEA-sopivuusindeksin estimaatti on 0,189; sen 90 %:n luottamusväli on 0,185-0,193 ja todennäköisyys, että RMSEA ≤ 0,05; on alle 0,001. CFI ja TLI ovat vastaavasti 0,929 ja 0,882.
Kahden faktorin mallin sopivuus aineistoon on kuitenkin hyvä. Tosin tässäkin tapauksessa suuren otoskoon vuoksi χ²-testin tulokset viittaavat mallin eroavan ideaalista mallista tilastollisesti merkitsevästi: χ²(8) = 1242,04; p < 0,001. RMSEA-sopivuusindeksin estimaatti sekä sen 90 %:n luottamusväli ja todennäköisyys, että RMSEA ≤ 0,05; ovat tässä järjestyksessä kolmen desimaalin tarkkuudella 0,092; 0,087–0,096 ja 0,000. Mallin CFI ja TLI ovat 0,985 ja 0,972; jotka viittaavat todella hyvään mallin sopivuuteen. Lisäksi koska kyseisen mallin jokainen faktorilataus oli korkea (> 0,6) ja erosi tilastollisesti merkitsevästi nollasta, voidaan päätellä, että kahden faktorin malli on parempi malli ja Lukukäsite ja Laskusujuvuus muodostavat kaksi erillistä kokonaisuutta FUNA-DB-testissä.
Kuva 2
FUNA-DB:n konfirmatorinen faktorianalyysi: kahden faktorin mallin polkukuvio
Huom. N = 18 405. LK = Lukukäsite-faktori; LS = Laskusujuvuus-faktori. Estimointimenetelmänä käytettiin täyden informaation suurimman uskottavuuden menetelmää (engl. full information maximum likelihood, FIML). Parametriestimaatit ovat standardoituja ja latenttien faktorien varianssit on asetettu ykkösiksi. Keskivirheet ovat suluissa parametriestimaattien vieressä. Kaikki parametriestimaatit erosivat tilastollisesti merkitsevästi nollasta. Faktorien Lukukäsite ja Laskusujuvuus välinen negatiivinen korrelaatio johtuu osatesteistä F1.1-F1.2 ja osatesteistä F2.1-F3.3 laskettujen pisteiden tulkinnallisesta erosta.
Taulukko 9
FUNA-DB:n konfirmatiivinen faktorianalyysi: yhden ja kahden faktorin mallien sopivuusindeksit
Huom. χ² = Khiin neliön testisuureen arvo; Va = vapausasteet; RMSEA = Root Mean Square Error of Approximation; Est. = RMSEA-estimaatti; 90 % lv = 90 prosentin luottamusväli RMSEA:lle; P(Est. ≤ 0,05) = todennäköisyys, että RMSEA on pienempi tai yhtä suuri kuin 0,05; CFI = Comparative Fit Index -estimaatti; TLI = Tucker-Lewis Index -estimaatti.
2.2.2 Kulttuurien välinen validiteetti (cross-cultural validity)
Seuraavaksi analysoidaan, toteutuuko FUNA-DB:n kulttuurien välinen validiteetti (engl. cross-cultural validity) tarkastelemalla testin kahden faktorin rakennevaliditeettia erikseen suomenkielisten ja ruotsinkielisten koulujen lapsille. Toteutamme FUNA-DB:n CFA-analyysi erikseen suomenkielisistä ja ruotsinkielisistä lapsista koostuville osa-aineistoille. Tämän lisäksi tutkitaan, onko FUNA-DB:n faktorirakenne samankaltainen eli invariantti suomen- ja ruotsinkielisten koulujen lasten aineistoissa, ja jos on, niin näiden osa-aineistojen latentteja keskiarvoja eli Lukukäsite- ja Laskusujuvuus-faktorien keskiarvoja voidaan vertailla ja faktoripisteiden yhteyttä koulun kieleen voidaan tutkia mielekkäästi. Mittausinvarianssia testataan tutkimalla konfiguraalisen, metrisen ja skalaarisen mallin RMSEA- ja CFI-sopivuusindeksien eroja (Chen, 2007; Meade et al., 2008). Konfiguraalinen malli on ryhmitelty malli ilman lisärajoituksia. Metrinen malli on ryhmitelty malli, jossa faktorilataukset on asetettu yhtä suuriksi ryhmien välillä. Skalaarinen malli on ryhmitelty malli, jossa sekä faktorilataukset että indikaattorien keskiarvot on asetettu yhtä suuriksi ryhmien välillä.
Aloitetaan tekemällä CFA-analyysi suomen- ja ruotsinkielisten koulujen lapsille erikseen. Kummankin mallin sopivuus aineistoon on hyväksyttävä (Taulukko 10). Erityisesti ruotsinkielisten koulujen lasten mallin sopivuus on todella hyvä (esimerkiksi RMSEA = 0,079 < 0,08). Sen sijaan suomenkielisten koulujen lasten mallin sopivuus ei eroa kokonaismallin sopivuudesta juuri lainkaan. Konfiguraalinen invarianssi toteutuu, mikä tarkoittaa sitä, että testin faktorirakenne on samanlainen suomen- ja ruotsinkielisten koulujen lasten aineistojen välillä.
Taulukko 10
Suomen- ja ruotsinkielisten koulujen lasten kahden faktorin mallien sopivuusindeksit
Huom. χ² = Khiin neliön testisuureen arvo; Va = vapausasteet; RMSEA = Root Mean Square Error of Approximation; Est. = RMSEA-estimaatti; 90 % lv = 90 prosentin luottamusväli RMSEA:lle; P(Est. ≤ 0,05) = todennäköisyys, että RMSEA on pienempi tai yhtä suuri kuin 0,05; CFI = Comparative Fit Index -estimaatti; TLI = Tucker-Lewis Index -estimaatti.
Kun testataan, toteutuuko heikko invarianssi, eli vertaillaan metristä ja konfiguraalista mallia keskenään, erot RMSEA- ja CFI-indekseissä kolmen desimaalin tarkkuudella ovat pieniä: ΔRMSEA = 0,009 ja ΔCFI = 0,000. Voidaan siis päätellä, että heikko invarianssi toteutuu. Kun testataan, toteutuuko vahva invarianssi, niin skalaarista mallia verrataan sekä konfiguraaliseen että metriseen malliin. Kun verrataan konfiguraalista ja skalaarista mallia, ΔRMSEA = 0,013 ja ΔCFI = 0,001. Kun verrataan metristä ja skalaarista mallia, ΔRMSEA = 0,004 ja ΔCFI = 0,001. Erot RMSEA- ja CFI-indekseissä ovat siis tässäkin tapauksessa pieniä ja vahva invarianssi toteutuu. Koska sekä konfiguraalinen, heikko että vahva invarianssi toteutuu, voidaan todeta, että FUNA-DB on invariantti suomen- ja ruotsinkielisten koulujen lasten aineistossa, ja täten suomen- ja ruotsinkielisten lasten latentteja keskiarvoja voidaan vertailla ja faktoripisteiden ja koulun kielen välistä yhteyttä voidaan tutkia tarkemmin. Tämä tehdään luvussa 3.
2.2.3 Ryhmien erotteluvaliditeetti (known-group validity)
Sukupuoli
Tutkitaan seuraavaksi FUNA-DB:n ryhmien erotteluvaliditeettia (engl. know-group validity) tarkastelemalla onko FUNA-DB:n faktorirakenne samanlainen tytöillä ja pojilla. Tämän lisäksi tutkitaan, onko FUNA-DB:n faktorirakenne invariantti sukupuolten yli. Aloitetaan toteuttamalla CFA-analyysi sukupuolittain. Tyttöjen ja poikien mallien sopivuusindeksit osoittavat, että kummankaan mallin sopivuus ei eroa kokonaismallin sopivuudesta juuri lainkaan (Taulukko 11). Täten konfiguraalinen invarianssi toteutuu ja testin faktorirakenne on samanlainen sukupuolten välillä.
Taulukko 11
Tyttöjen ja poikien kahden faktorin mallien sopivuusindeksit
Huom. χ² = Khiin neliön testisuureen arvo; Va = vapausasteet; RMSEA = Root Mean Square Error of Approximation; Est. = RMSEA-estimaatti; 90% lv = 90 prosentin luottamusväli RMSEA:lle; P(Est. ≤ 0,05) = todennäköisyys, että RMSEA on pienempi tai yhtä suuri kuin 0,05; CFI = Comparative Fit Index -estimaatti; TLI = Tucker-Lewis Index -estimaatti.
Tutkitaan seuraavaksi, toteutuvatko heikko ja vahva invarianssi, kun aineisto ryhmitellään sukupuolittain. Konfiguraalisen ja metrisen mallien erot RMSEA- ja CFI-indekseissä ovat ΔRMSEA = 0,008 ja ΔCFI = 0,001. Skalaarisen mallin erot konfiguraaliseen sekä metriseen malliin RMSEA- ja CFI-indekseissä ovat vastaavasti ΔRMSEA = 0,005 ja ΔCFI = 0,011 ja ΔRMSEA = 0,013 ja ΔCFI = 0,010. Erot ovat pieniä, joten heikko ja vahva invarianssi toteutuvat. Tyttöjen ja poikien latentteja keskiarvoja voidaan vertailla mielekkäästi ja faktoripisteiden yhteyttä sukupuoleen voidaan tutkia tarkemmin (Luku 3).
Luokka-aste
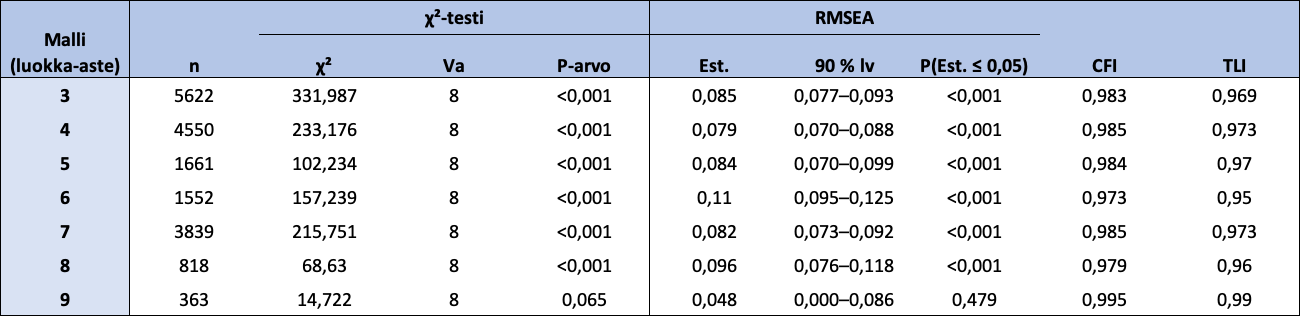
Tutkitaan seuraavaksi FUNA-DB:n ryhmien erotteluvaliditeettia (engl. know-group validity) koskien myös luokka-asteita ja tutkitaan, onko FUNA-DB:n faktorirakenne samanlainen luokka-asteilla 3-9. Tämän lisäksi tutkitaan, onko FUNA-DB:n faktorirakenne invariantti eri luokka-asteilla. Aloitetaan toteuttamalla CFA-analyysi luokka-asteittain. Eri luokka-asteiden mallien sopivuusindeksit näkyvät taulukossa 12. 6-luokkalaisten mallin sopivuus on huonoin (RMSEA = 0,110 > 0,1). Siitä huolimatta FUNA-DB:n kahden faktorin rakenne toimii myös eri luokka-asteilla ja konfiguraalinen invarianssi toteutuu.
Taulukko 12
Luokka-asteiden 3-9 lasten kahden faktorin mallien sopivuusindeksit
Huom. χ² = Khiin neliön testisuureen arvo; Va = vapausasteet; RMSEA = Root Mean Square Error of Approximation; Est. = RMSEA-estimaatti; 90% lv = 90 prosentin luottamusväli RMSEA:lle; P(Est. ≤ 0,05) = todennäköisyys, että RMSEA on pienempi tai yhtä suuri kuin 0,05; CFI = Comparative Fit Index -estimaatti; TLI = Tucker-Lewis Index -estimaatti.
Tutkitaan seuraavaksi, toteutuvatko heikko ja vahva invarianssi, kun aineisto ryhmitellään luokka-asteittain. Konfiguraalisen ja metrisen mallin erot RMSEA- ja CFI-indekseissä ovat pieniä: ΔRMSEA = 0,011 ja ΔCFI = 0,001. Skalaarisen mallin erot konfiguraaliseen sekä metriseen malliin RMSEA- ja CFI-indekseissä ovat vastaavasti ΔRMSEA = 0,008; ΔCFI = 0,020 ja ΔRMSEA = 0,019; ΔCFI = 0,019. Erot ovat tässäkin tapauksessa hyväksyttävän suuruisia, joten heikko ja vahva invarianssi toteutuvat, ja eri luokka-asteiden lasten latentteja keskiarvoja voidaan vertailla mielekkäästi ja faktoripisteiden yhteyttä luokka-asteeseen voidaan tutkia tarkemmin (Luku 3).
2.2.4 Pitkittäinen mittausinvarianssi
Hakkarainen et al. (2025) tutkivat FUNA-DB:n pitkittäistä mittausinvarianssia kahden aikapisteen (2-4 viikon väli) suhteen CFA-analyysillä; he tarkastelivat konfiguraalisen, metrisen ja skalaarisen mallin eroja CFI- ja RMSEA-sopivuusindekseissä. Tulosten perusteella sekä metrinen että skalaarinen invarianssi toteutui aikapisteiden välillä, joten FUNA-DB:n kahden faktorin rakenne säilyi ajan suhteen ja pitkittäinen mittausinvarianssi toteutui. Tämän perusteella FUNA-DB:tä voidaan käyttää havaitsemaan kehityksellisiä muutoksia Lukukäsitteessä ja Laskusujuvuudessa luotettavasti.
2.2.5 Osatestien välinen yhtenevä validiteetti (convergent validity)
FUNA-DB:n osatestien välinen yhtenevä validiteetti (engl. convergent validity) nähdään tarkastelemalla osatestien välisiä korrelaatioita, jotka näkyvät taulukossa 13. Erityisesti saman faktorin osatestien välisten korrelaatioiden pitäisi olla suuria (> 0,6), ja tässä tapauksessa ne ovatkin. Osatestien F1.1 ja F1.2 välinen korrelaatio on 0,681 ja osatestien F2.1-F3.3 väliset korrelaatiot ovat kaikki yli 0,7. Myös eri kokonaisuuksien osatestien väliset korrelaatiot ovat itseisarvoltaan melko suuria (> 0,45), joten korrelaatiotarkastelujen perusteella osatestien yhtenevä validiteetti toteutuu.
Taulukko 13
FUNA-DB:n osatestien väliset korrelaatiot
Huom. Kaikki osatestien väliset korrelaatiot ovat tilastollisesti merkitseviä merkitsevyystasolla 0,001. Eri kokonaisuuksien osatestien väliset negatiiviset korrelaatiot johtuvat osatesteistä laskettujen pisteiden tulkinnallisesta erosta.
2.2.6 Lukukäsite-kokonaisuuden rinnakkaisvaliditeetti (concurrent validity)
Tutkitaan Lukukäsite-kokonaisuuden rinnakkaisvaliditeettia (engl. concurrent validity) suhteessa Laskusujuvuuteen. Ensin toteutetaan ROC-analyysi koko aineistolle, minkä tarkoituksena on selvittää, pystyykö suoriutumisella Lukukäsitteen osatesteissä luokittelemaan ne lapset, joilla on matemaattinen oppimisvaikeus (n. 5 % aineistosta, jatkossa MLD-lapset, engl. mathematical learning disabilities), ja ne lapset, joilla ei ole matemaattista oppimisvaikeutta (jatkossa ei-MLD-lapset), perustuen Laskusujuvuuden osatesteissä suoriutumiseen. Tämän lisäksi tutkitaan Lukukäsitteen kykyä luokitella ne lapset, joiden suoriutuminen oli matalalla tasolla muihin verrattuna (n. 25 % aineistosta, jatkossa LA-lapset, engl. low achievement), ja ne lapset, joilla suoriutuminen oli LA-lapsia korkeammalla tasolla (jatkossa ei-LA-lapset). Koko aineiston ROC-analyysien jälkeen toteutetaan ROC-analyysit erikseen luokka-asteiden 3-4, 5-6 ja 7-9 lapsille, minkä tarkoitus on selvittää, eroaako Lukukäsite-kokonaisuuden luokittelukyky kyseisten luokka-asteryhmien välillä. ROC-analyysien toteuttamisessa käytetään R-ohjelman pROC-pakettia (Robin et al., 2011). Jotta käyrät saadaan piirrettyä, Laskusujuvuus-kokonaisuudelle lasketaan kaksi binääristä muuttuja, joista toinen saa arvon 1, kun standardoiduista pisteistä lasketun Laskusujuvuus-summamuuttujan [1] arvo on pienempi tai yhtä suuri kuin 5-persentiili kyseessä olevassa luokka-asteryhmässä (MLD-lapset) ja arvon 0 muulloin (ei-MLD-lapset), ja toinen saa vastaavasti arvon 1, kun Laskusujuvuus-summamuuttujan arvo on pienempi tai yhtä suuri kuin 25-persentiili kyseessä olevassa luokka-asteryhmässä (LA-lapset) ja arvon 0 muulloin (ei-LA-lapset).
Kun binääriset Laskusujuvuus-muuttujat on muodostettu, niitä käytetään vastemuuttujina ROC-käyrien piirtämisessä. Luokittelevana muuttujana käytetään vastaavasti aina kyseessä olevan luokka-asteryhmän standardoiduista pisteistä laskettua Lukukäsite-summamuuttujaa [2] . ROC-käyrä näyttää luokittelumallin suorituskyvyn kuvaamalla sensitiivisyys- (engl. sensitivity tai true positive rate, TPR) ja spesifisyysparametrien (engl. specificity tai true negative rate, TNR) välistä yhteyttä eri kynnysarvoilla, jotka määräävät sen, millä luokittelevan muuttujan arvoilla lapset luokitellaan MLD- ja ei-MLD-lapsiin tai vastaavasti LA- ja ei-LA-lapsiin. Sensitiivisyys tarkoittaa tässä tapauksessa Laskusujuvuuden osatesteistä suoriutumisen perusteella kaikkien oikeiden MLD-lasten (LA-lasten) lukumäärästä niiden lasten suhteellista osuutta, joiden luokittelumalli on myös luokitellut olevan MLD-lapsiin (LA-lapsia) [3] . Sensitiivisyys lasketaan kaavalla TP/(TP+FN), jossa TP eli True Positive (aito positiivinen) on vastemuuttujan oikein luokiteltujen arvojen 1 lukumäärä, eli tässä tapauksessa niiden lasten lukumäärä, jotka on luokiteltu MLD-lapsi (LA-lapsi) ja ovat myös oikeasti MLD-lapsia (LA-lapsia) perustuen Laskusujuvuuden osatesteistä suoriutumiseen. FN eli False Negative (väärä negatiivinen) on vastemuuttujan väärin luokiteltujen arvojen 0 lukumäärä, eli tässä tapauksessa niiden lasten lukumäärä, jotka on luokiteltu olevan ei-MLD-lapsia (ei-LA-lapsia) mutta ovat oikeasti MLD-lapsia (LA-lapsia). TP + FN on siis kaikkien oikeiden MLD-lasten (LA-lasten) lukumäärä.
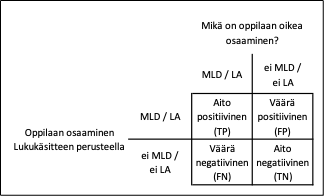
Kuva 3
Esitys aidon positiivisen (TP), väärän positiivisen (FP), aidon negatiivisen (TN) ja väärän negatiivisen (FN) luokittelusta
Huom. MLD = mathematical learning disability eli matemaattinen oppimisvaikeus; LA = low achievement eli matala suoriutuminen.
Spesifisyys tarkoittaa tässä tapauksessa Laskusujuvuuden osatesteistä suoriutumisen perusteella kaikkien oikeasti ei-MLD-lasten (tai ei-LA-lasten, kun 25 persentiilin raja) lukumäärästä niiden lasten suhteellista osuutta, joiden luokittelumalli on myös luokitellut ei-MLD-lapsiksi (tai ei-LA-lapseksi) [4] . Spesifisyys lasketaan kaavalla TN/(TN+FP), jossa TN eli True Negative (aito negatiivinen) on vastemuuttujan oikein luokiteltujen arvojen 0 lukumäärä, eli tässä tapauksessa niiden lasten lukumäärä, jotka on luokiteltu ei-MLD-lapsiin (tai ei-LA-lapsiin), ja jotka ovat myös oikeasti ei-MLD-lapsia (tai ei-LA-lapsia) perustuen Laskusujuvuuden osatesteistä suoriutumiseen. FP eli False Positive (väärä positiivinen) on vastemuuttujan väärin luokiteltujen arvojen 1 lukumäärä, eli tässä tapauksessa niiden lasten lukumäärä, jotka on luokiteltu MLD-lapsiin (tai LA-lapsiin), mutta ovat oikeasti ei-MLD-lapsia (tai ei-LA-lapsia). TN + FP on siis kaikkien oikeiden ei-MLD-lasten (tai ei-LA-lasten) lukumäärä. Kuva 3 esittää TP:n, FP:n, TN:n ja FN:n luokittelutaulukkoa.
Kullekin ROC-käyrälle lasketaan AUC-parametrin (engl. area under the curve) arvo eli käyrän alle jäävä pinta-ala, jonka arvojoukko on [0, 1]. Luokittelumalli, jonka ROC-käyrän AUC on 1, luokittelee lapsista 100 % oikein. Sen sijaan luokittelumalli, jonka ROC-käyrän AUC on 0,5; vastaa kolikonheittotilannetta (arpomista), ja kyseinen malli on tällöin täysin hyödytön luokittelumallina. Jos AUC on välillä 0,7-0,8; malli on kohtalainen luokittelija, ja jos se on välillä 0,8-0,9; mallin luokittelukykyä voidaan pitää hyvänä. Sen sijaan, jos AUC on välillä 0,9-1; mallin luokittelukyky on erinomainen (Bozikov & Lijana, 2010).
ROC-käyrien ja niiden AUC-arvojen lisäksi tutkitaan, kuinka Lukukäsitteen luokittelukyky vaihtelee, kun Lukukäsitteellä käytetään luokittelukynnysarvoina 5- ja 25-persentiilejä. Näitä persentiilejä käyttäen lasketaan sensitiivisyys-, spesifisyys-, PPV-, NPV- ja tarkkuusparametrien arvot koko aineistolle ja luokka-asteryhmittäin. PPV-parametrin (engl. positive predictive value) arvo kuvastaa todennäköisyyttä, että MLD-lapseksi (LA-lapseksi) luokiteltu lapsi on oikeasti MLD-lapsi (LA-lapsi) (PPV = TP / (TP + FP)). NPV-parametrin (engl. negative predictive value) arvo kuvastaa todennäköisyyttä, että ei-MLD-lapseksi (ei-LA-lapseksi) luokiteltu lapsi on oikeasti ei-MLD-lapsi (ei-LA-lapsi) (NPV = TN / (FN + TN))). Tarkkuusparametrin (engl. accuracy) arvo kertoo kaikkien oikein luokiteltujen lasten osuuden kaikista lapsista kyseessä olevassa luokka-asteryhmässä (tarkkuus = (TP + TN) / (TP + TN + FP + FN)) (Bozikov & Lijana, 2010).
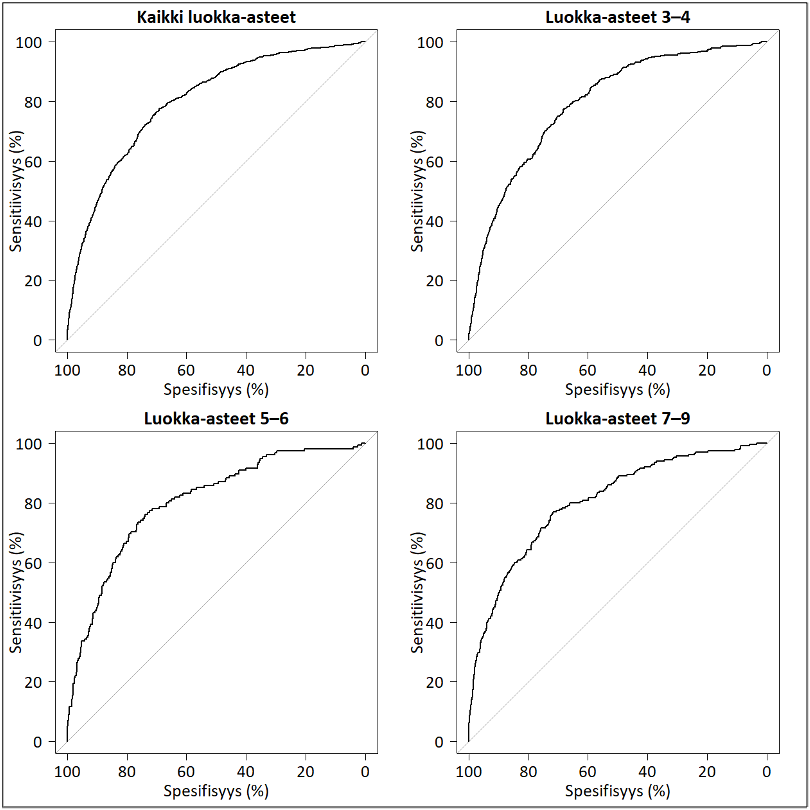
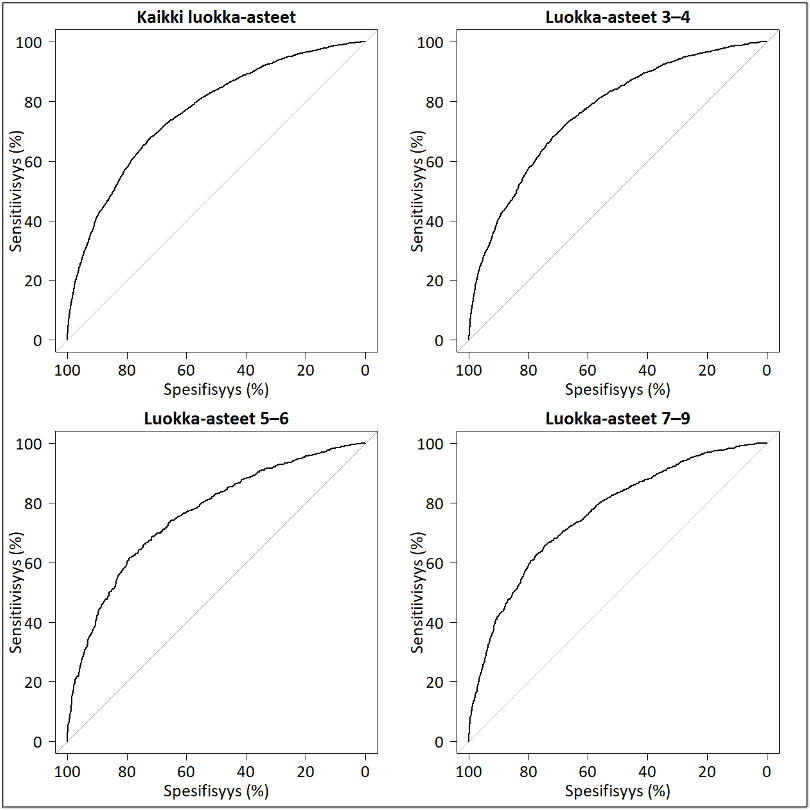
Tarkastellaan seuraavaksi edellä kuvattujen ROC-analyysien tuloksia. ROC-käyrät liittyen Lukukäsitteen luokittelukykyyn matemaattisten oppimisvaikeuksien (MLD- ja ei-MLD) sekä matalan suoriutumisen (LA- ja ei-LA) tunnistamisessa näkyvät kuvissa 4 ja 5. Koko aineiston ROC-käyrät ja niiden AUC-arvot osoittavat, että Lukukäsite-kokonaisuuden luokittelukyky sekä MLD:ssä että LA:ssa on vähintäänkin kohtalainen. Sen sijaan luokka-asteryhmittäiset ROC-käyrät ja niiden AUC-arvot osoittavat, että Lukukäsitteen luokittelukyvyssä ei ole eroa luokka-asteryhmittäin. Näiden havaintojen perusteella Lukukäsitteen rinnakkaisvaliditeetti FUNA-DB:ssä toteutuu.
Kuva 4
Lukukäsitteen luokittelukyky matemaattisten oppimisvaikeuksien tunnistamisessa: luokka-asteryhmittäiset sekä koko aineiston ROC-käyrät
Huom. Puuttuvien arvojen poistamisen jälkeen, oppilasmäärät luokka-asteryhmittäin olivat 9452 (luokka-asteet 3-4), 3067 (luokka-asteet 5-6) ja 4669 (luokka-asteet 7-9). Käyrien alapuolella olevat pinta-alat eli AUC-arvot olivat 79,9 % (kaikki), 79,6 % (3-4), 80,3 % (5-6) ja 80,4 % (7-9).
Kuva 5
Lukukäsitteen luokittelukyky matalan suoriutumisen tunnistamisessa: luokka-asteryhmittäiset sekä koko aineiston ROC-käyrät
Huom. Puuttuvien arvojen poistamisen jälkeen, oppilasmäärät luokka-asteryhmittäin olivat 9452 (luokka-asteet 3-4), 3067 (luokka-asteet 5-6) ja 4669 (luokka-asteet 7-9). Käyrien alapuolella olevat pinta-alat eli AUC-arvot olivat 76,3 % (kaikki), 76,5 % (3-4), 76,1 % (5-6) ja 76,1 % (7-9).
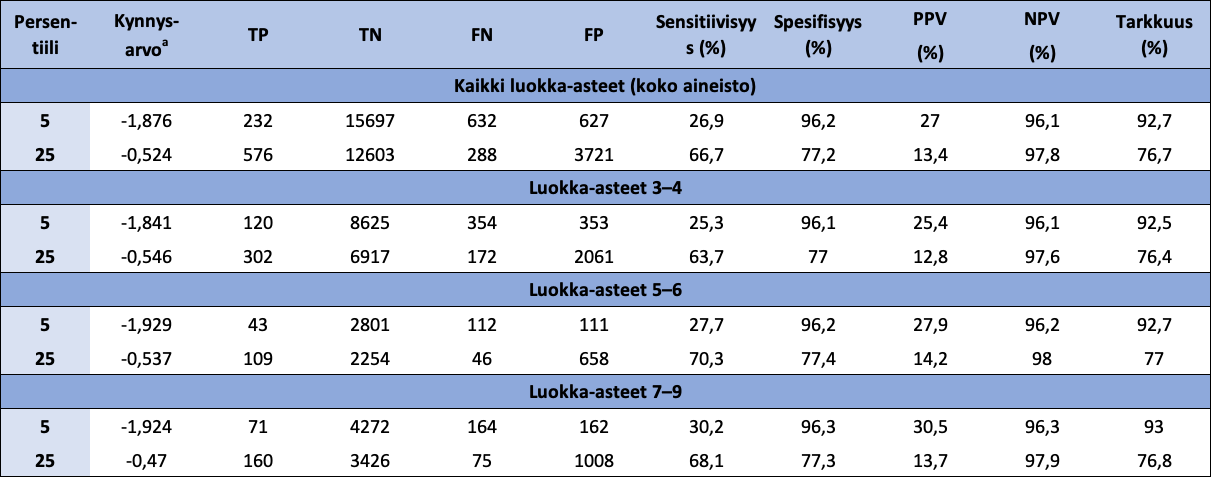
Tarkastellaan vielä taulukoita 14 ja 15, joissa esitetään Lukukäsitteen luokittelukykyä matemaattisten oppimisvaikeuksien (Laskusujuvuuden kynnysarvo 5-persentiilissä; taulukko 14) sekä matalan suoriutumisen (Laskusujuvuuden kynnysarvo 25-persentiilissä; taulukko 15) tunnistamisessa kuvaavat parametriarvot, kun luokittelussa sen kynnysarvoina käytetään 5- ja 25-persentiilejä. Taulukkojen perusteella Lukukäsitteen luokittelun tarkkuus laskee sekä MLD:n että LA:n suhteen kaikilla luokka-asteryhmillä, kun kynnysarvoa kasvatetaan 5-persentiilistä 25-persentiiliin. Tämä lasku on erityisen suuri, kun yritetään havaita MLD-lapset. Vastaava havainto voidaan tehdä PPV-parametrin suhteen, mikä tarkoittaa, että Lukukäsitteen tunnistamista MLD-lapsista ja LA-lapsista suurempi osa on oikein silloin, kun Lukukäsitteen kynnysarvo on 5-persentiilissä kuin silloin, kun kynnysarvo on 25-persentiilissä. Kaiken kaikkiaan ROC-analyysien tulosten perusteella Lukukäsite pystyy tunnistamaan MLD-lapset paremmin kuin LA-lapset sekä koko oppilasmassasta että luokka-asteryhmittäin.
Taulukko 14
Lukukäsitteen luokittelukykyä matemaattisten oppimisvaikeuksien tunnistamisessa (Laskusujuvuuden kynnysarvo 5-persentiilissä) kuvaavat parametriarvot, kun luokittelussa sen kynnysarvoina käytetään 5- ja 25-persentiilejä koko aineistossa sekä luokka-asteryhmittäin
Huom. Puuttuvien arvojen poistamisen jälkeen, oppilasmäärät luokka-asteryhmittäin olivat 9452 (luokka-asteet 3-4), 3067 (luokka-asteet 5-6) ja 4669 (luokka-asteet 7-9). a Standardoiduista pisteistä lasketun Lukukäsite-summamuuttujan arvo. TP = aito positiivinen; TN = aito negatiivinen; FN = väärä negatiivinen; FP = väärä positiivinen; PPV = positive predictive value; NPV = negative predictive value.
Taulukko 15
Lukukäsitteen luokittelukykyä matalan suoriutumisen tunnistamisessa (Laskusujuvuuden kynnysarvo 25-persentiilissä) kuvaavat parametriarvot, kun luokittelussa sen kynnysarvoina käytetään 5- ja 25-persentiilejä koko aineistossa sekä luokka-asteryhmittäin
Huom. Puuttuvien arvojen poistamisen jälkeen, oppilasmäärät luokka-asteryhmittäin olivat 9452 (luokka-asteet 3-4), 3067 (luokka-asteet 5-6) ja 4669 (luokka-asteet 7-9). a Standardoiduista pisteistä lasketun Lukukäsite-summamuuttujan arvo. TP = aito positiivinen; TN = aito negatiivinen; FN = väärä negatiivinen; FP = väärä positiivinen; PPV = positive predictive value; NPV = negative predictive value.
2.2.7 Yhtenevä validiteetti (convergent validity) RMAT-testin suhteen
FUNA-DB:n yhtenevän validiteetin (engl. convergent validity) tarkastelu tehtiin Hakkaraisen et al. (2025) raportissa. Hakkaraisen et al. (2025) tutkimukseen osallistuneet lapset suorittivat FUNA-DB:n lisäksi kynällä ja paperilla tehtävän RMAT-testin. Hakkarainen et al. (2025) laskivat korrelaation FUNA-DB:n Lukukäsitteen ja RMAT-testin (r = -0.69) välillä sekä Laskusujuvuuden ja RMAT-testin (r = 0.81) välillä ensimmäisessä mittauspisteessä. Koska kummallakin faktorilla oli korkea korrelaatio RMAT-testin kanssa, FUNA-DB:n yhtenevä validiteetti toteutui.
3 Faktoripisteiden yhteys koulun kieleen, sukupuoleen ja luokka-asteeseen
Tässä luvussa tutkitaan kahden faktorin mallin (Lukukäsite ja Laskusujuvuus) faktoripisteiden yhteyttä taustamuuttujiin eli koulun kieleen, sukupuoleen sekä luokka-asteeseen regressiomallien avulla. Sitä ennen vertaillaan latentteja keskiarvoja eli Lukukäsite- ja Laskusujuvuus-faktorien keskiarvoja FUNA-DB:ssä kieliryhmittäin, sukupuolittain sekä luokka-asteittain. Tämän tarkoitus on pohjustaa regressiomallien tutkimista ja näyttää, että faktoripisteillä ylipäätänsä voi olla jonkinlainen yhteys taustamuuttujiin. Latenttien keskiarvojen vertailut eivät kuitenkaan ota huomioon taustamuuttujien interaktiovaikutuksia, joten ne eivät esimerkiksi kerro sitä, miten suomen- ja ruotsinkielisten koulujen lasten tai sukupuolien välinen mahdollinen ero muuttuu luokka-asteen kasvaessa.
Suomen- ja ruotsinkielisten lasten latenttien keskiarvojen vertailu
Vertaillaan suomen- ja ruotsinkielisten koulujen lasten latentteja keskiarvoja FUNA-DB:ssä. Tämä voidaan tehdä ryhmitellyn mallin konfirmatorisen faktorianalyysin tulosten perusteella. Suomenkielisten koulujen lasten malli on tässä tapauksessa vertailumalli, johon ruotsinkielisten koulujen lasten mallia verrataan, joten suomenkielisten koulujen lasten standardoidut faktorikeskiarvot on asetettu nolliksi. Huomataan, että ruotsinkielisten koulujen lasten Lukukäsite- ja Laskusujuvuus-faktorien standardoidut keskiarvot ovat tässä järjestyksessä -0,026 ja 0,206; joista vain Laskusujuvuus-faktorin keskiarvo eroaa tilastollisesti merkitsevästi nollasta (p-arvot ovat kolmen desimaalin tarkkuudella Lukukäsite: 0,361 ja Laskusujuvuus: 0,000). Toisin sanoen ruotsinkielisten koulujen lasten Laskusujuvuus-faktorin keskiarvo eroaa tilastollisesti merkitsevästi suomenkielisten koulujen lasten Laskusujuvuus-faktorin keskiarvosta.
Tyttöjen ja poikien latenttien keskiarvojen vertailu
Vertaillaan seuraavaksi sukupuolten latentteja keskiarvoja. Tyttöjen malli on tässä tapauksessa vertailumalli. Poikien Lukukäsite- ja Laskusujuvuus-faktoreiden standardoidut keskiarvot ovat tässä järjestyksessä -0,053 ja 0,320; jotka molemmat eroavat tilastollisesti merkitsevästi nollasta merkitsevyystasolla 0,01 (p-arvot ovat kolmen desimaalin tarkkuudella Lukukäsite: 0,003 ja Laskusujuvuus: 0,000), eli poikien latentit keskiarvot eroavat tilastollisesti merkitsevästi tyttöjen latenteista keskiarvoista.
Eri luokka-asteiden lasten latenttien keskiarvojen vertailu
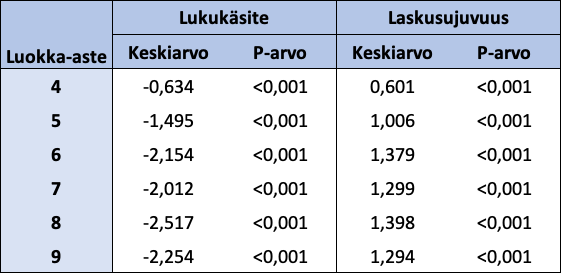
Vertaillaan seuraavaksi eri luokka-asteiden lasten latentteja keskiarvoja. 3-luokkalaisten malli on tässä tapauksessa vertailumalli. Muiden luokka-asteiden Lukukäsite- ja Laskusujuvuus-faktorien standardoidut keskiarvot näkyvät taulukossa 16. Jokaisen luokka-asteen (4–9) molemmat latentit keskiarvot eroavat 3-luokkalaisten latenteista keskiarvoista tilastollisesti merkitsevästi merkitsevyystasolla 0,001. Jokaisen luokka-asteen kohdalla Lukukäsite-faktorin keskiarvo on negatiivinen ja Laskusujuvuus-faktorin keskiarvo on positiivinen.
Taulukko 16
Luokka-asteiden 4-9 standardoidut latentit keskiarvot ja keskiarvojen p-arvot
Regressiomallit
Latenttien keskiarvojen vertailut osoittivat, että koulun kielellä, sukupuolella ja luokka-asteella on yhteyttä FUNA-DB-osatesteistä suoriutumiseen. Tutkitaan tätä tarkemmin tekemällä regressiomallinnus, jossa selitettävinä muuttujina ovat Lukukäsitteen ja Laskusujuvuuden faktoripisteet ja selittäjinä taustamuuttujat eli koulun kieli, sukupuoli sekä luokka-aste (malli 1). Tämä malli selittää 33,4 % Lukukäsitteen varianssista ja 28,1 % Laskusujuvuuden varianssista. Merkitsevyystasolla 0,05 Lukukäsitteen ainut ei tilastollisesti merkitsevä selittävä muuttuja on sukupuoli. Laskusujuvuuden kaikki selittäjät ovat tilastollisesti merkitseviä merkitsevyystasolla 0,001. Estimoitujen standardoitujen regressiokertoimien perusteella ruotsinkielisten koulujen lapset pärjäsivät heikommin Lukukäsitteen (β = 0,02; p-arvo = 0,018) osatesteissä mutta paremmin Laskusujuvuuden (β = 0,04; p-arvo < 0,001) osatesteissä kuin suomenkielisten koulujen lapset. Pojat pärjäsivät paremmin Laskusujuvuuden (β = 0,164; p-arvo < 0,001) osatesteissä kuin tytöt. Luokka-asteella on suurin yhteys faktoripisteisiin: vanhemmat lapset saivat parempia pisteitä sekä Lukukäsitteessä (β = -0,578; p-arvo < 0,001) että Laskusujuvuudessa (β = 0,500; p-arvo < 0,001) kuin nuoremmat. Tämän mallin sopivuusindeksit näkyvät taulukossa 17.
Sovitetaan aineistoon lisäksi malli (malli 2), jossa ovat mukana taustamuuttujien lisäksi niiden interaktiotermit. Tämä malli selittää 33,7 % Lukukäsitteen varianssista ja 28,2 % Laskusujuvuuden varianssista. Lukukäsitteen tapauksessa sukupuoli sekä koulun kielen ja sukupuolen interaktiotermi eivät ole tilastollisesti merkitseviä selittäjiä merkitsevyystasolla 0,05. Laskusujuvuuden tapauksessa koulun kieli sekä koulun kielen ja sukupuolen interaktiotermi eivät ole tilastollisesti merkitseviä selittäjiä merkitsevyystasolla 0,05. Molempien faktorien tapauksessa koulun kielen ja luokka-asteen sekä sukupuolen ja luokka-asteen interaktiotermit ovat tilastollisesti merkitseviä merkitsevyystasolla 0,001. Lukukäsitteen selittäjinä interaktiotermien estimoidut regressiokertoimet ovat β = -0,162 (koulun kieli * luokka-aste) ja β = 0,126 (sukupuoli * luokka-aste), jotka osoittavat, että suomen- ja ruotsinkielisten koulujen lasten välinen ero suomenkielisten koulujen hyväksi pienenee luokka-asteen mukaan ja sukupuolten välinen ero kasvaa tyttöjen hyväksi luokka-asteen mukaan. Laskusujuvuuden selittäjinä niiden estimoidut regressiokertoimet ovat β = 0,123 (koulun kieli * luokka-aste) ja β = -0,093 (sukupuoli * luokka-aste), jotka osoittavat, että suomen- ja ruotsinkielisten koulujen välinen ero kasvaa luokka-asteen mukaan ruotsinkielisten koulujen hyväksi ja sukupuolten välinen ero poikien hyväksi pienenee luokka-asteen mukaan. Tämänkin mallin sopivuusindeksit näkyvät taulukossa 17.
Taulukko 17
Koulun kielen, sukupuolen ja luokka-asteen vaikutusta kahden faktorin mallin faktoripisteisiin tutkivien regressiomallien sopivuusindeksit
4 Oman opetusryhmän tulosten tarkastelu ViLLE:ssä
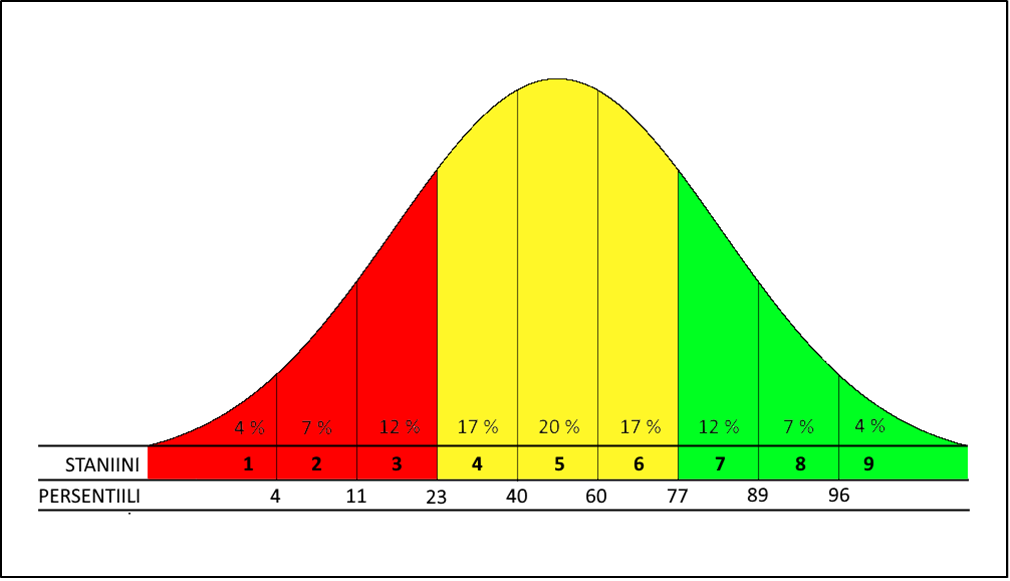
FUNA-DB:n ryhmä- ja lapsikohtaiset tulokset näkyvät ViLLE:ssä FUNA-analytiikkanäkymässä. FUNA-DB:n osatestit on rakennettu niin, että niiden pistejakaumat muodostavat kellokäyrän, mikä on tavallista taitoa mittaavissa testeissä. Tämä tarkoittaa sitä, että keskitasoisia lapsia on paljon ja ääripäiden lapsia eli joko todella taitavia tai todella heikkoja osaajia on vähemmän. Lasten tulosten sijoittumista kellokäyrälle kuvataan erilaisten pisteytysten avulla, ja tässä tapauksessa osatestien tulokset esitetään staniiniasteikolla (engl. stanine eli standard nine), jolloin pisteiden keskiarvo on 5 ja keskihajonta 2 (Kuva 5). Staniinipisteet saadaan, kun kellokäyrä jaetaan yhdeksään puolen keskihajonnan mittaiseen palaseen aloittaen keskeltä (pois lukien ensimmäinen ja viimeinen palanen, jotka ”jäävät yli” paloittelusta, eli ne ovat käyrän häntiä). Keskiarvon molemmilla puolilla on siten 0,25 keskihajontaa. FUNA-testipatteristo normitetaan valtakunnallisiin viiteaineistoihin, jolloin lasten staniinipisteet lasketaan aina suhteessa tämän viiteryhmän kellokäyrän muotoiseen tulokseen. FUNA:n analytiikkanäkymässä voi vaihtaa viiteryhmää, jolloin aina ei tarvitse verrata ryhmää tai lasta omaan luokka-asteeseen.
Staniinipisteitäa voidaan kuvata myös persentiileinä (Kuva 6). Persentiili on luku, joka kertoo, kuinka monta prosenttia otoksesta lapsista on suoriutunut kyseessä olevaa pistemäärää heikommin. Esimerkiksi 3 staniinipistettä tarkoittaa, että oppilaan suoritus kuuluu joukkoon, joka kuluu 11–23-persentiilin ryhmään, ja tällöin kyseinen oppilas on suoriutunut paremmin kuin heikoin 11 %, mutta heikommin kuin 77 % viiteryhmästä.
Kuva 6
Esitys staniiniasteikon mukaan jaetusta kellokäyrästä
Tulkintojen helpottamiseksi staniiniarvot on kuvattu numeroiden lisäksi värikoodeilla FUNA-analytiikkanäkymässä. Punainen väri vastaa staniinipisteitä 1–3 ja tarkoittaa keskimääräistä heikompaa suoritusta. Keltainen väri vastaa staniinipisteitä 4–6 ja tarkoittaa keskimääräistä suoritusta. Vihreä väri vastaa staniinipisteitä 7–9 ja tarkoittaa keskimääräistä parempaa suoritusta. Näiden lisäksi on harmaa väri, joka tarkoittaa, että lapsen suoritukset eivät ole arvioitavissa, mikä voi johtua esimerkiksi teknisestä virheestä tai siitä, että lapsi on yrittänyt vain arvata oikeita vastauksia tai lapsi ei ole ollut mukana testin tekemisessä.
ViLLE:ssä on kaksi erilaista analytiikkanäkymää: ryhmäkohtainen näkymä ja oppilasnäkymä. Ryhmänäkymässä näkyy valitulle osatestille ryhmän kunkin lapsen staniinipisteet suhteessa valitun viiteryhmän kellokäyrän muotoiseen tulokseen. Lisäksi koko ryhmän keskimääräisen suorituksen taso näkyy ryhmänäkymän yläosassa ympyrän sisällä olevana numerona ja ympyrän sisemmän renkaan värikoodina. Saman renkaan ulommassa renkaassa näkyy värikoodein vielä se, miten ryhmä on jakautunut hyvin suoriutuneisiin, keskivertaisesti suoriutuneisiin ja heikosti suoriutuneisiin oppilaisiin. Oppilasnäkymässä näkyy valitulle lapselle kustakin osatestistä saadut staniinipisteet suhteessa valitun viiteryhmän kellokäyrän muotoiseen tulokseen. Lisäksi valitun lapsen keskiarvot molemmille kokonaisuuksille (Lukukäsite ja Laskusujuvuus) ja koko FUNA-DB-testille näkyvät näkymän yläosassa kolmen ympyrän sisällä olevina numeroina ja ympyröiden sisempien renkaiden värikoodeina. Lisäksi samojen ympyröiden ulommissa renkaissa näkyvät valitun lapsen kokonaisuuksien ja koko testin osatestien pisteiden jakautuminen hyvään, keskivertaiseen ja heikkoon suoritukseen värikoodein. Osatestien ja ryhmänäkymän tulokset voi ladata omalle tietokoneelle joko PDF- tai Excel-tiedostona. Oppilasnäkymän tulokset voi ladata vain PDF-tiedostona.
Alaviitteet
[1] Laskusujuvuus-summamuuttuja muodostetaan laskemalla jokaisen lapsen osatestien F2.1, F3.1, F3.2 ja F3.3 standardoidut pisteet yhteen ja jakamalla saatu summa osatestien määrällä eli luvulla 4. Tässä tapauksessa standardoidut pisteet laskettiin luokka-astekohtaisesti.
[2] Lukukäsite-summamuuttuja muodostetaan laskemalla jokaisen lapsen osatestien F1.1 ja F1.2 standardoidut pisteet yhteen ja jakamalla saatu summa osatestien määrällä eli luvulla 2. Tässä tapauksessa standardoidut pisteet laskettiin luokka-astekohtaisesti.
[3] Vrt. Duodecim-terveyskirjaston määritelmä sensitiivisyydelle: https://www.terveyskirjasto.fi/ltt03075.
[4] Vrt. Duodecim-terveyskirjaston määritelmä spesifisyydelle: https://www.terveyskirjasto.fi/ltt03206.
Lähdeluettelo
Arbuckle, J. L. (1996). Full information estimation in the presence of incomplete data. Teoksessa G. A. Marcoulides, & R. E. Schumacker (Eds.), Advanced structural equation modelling (s. 243-277). Lawrence Erlbaum Associates, Inc.
Aunio, P. & Niemivirta, M. (2010). Predicting children’s mathematical performance in grade one by early numeracy. Learning and Individual Differences, 20(5), 427–435. https://doi.org/10.1016/j.lindif.2010.06.003
Blume, F., Dresler, T., Gawrilow, C., Ehlis, A. C., Goellner, R., and Moeller, K. (2021). Examining the relevance of basic numerical skills for mathematical achievement in secondary school using a within-task assessment approach. Acta Psychologica, 215(103289). https://doi.org/10.1016/j.actpsy.2021.103289
Bozikov, J., & Lijana, Z. K. (2010). Test validity measures and receiver operating characteristic (ROC) analysis. Teoksessa L. Zaletel-Kragelj, & J. Boţikov (Eds.), Methods and tools in public health: A handbook for teachers, researchers and health professionals (pp. 749-770). Hans Jacobs Publishing Company. Saatavissa: https://www.researchgate.net/publication/235328477_Test_Validity_Measures_and_Receiver_Operating_Characteristic_ROC_Analysis
Brannon, E. M., & Terrace, H. S. (1998). Ordering of the numerosities 1 to 9 by monkeys. Science, 282(5389), 746-749. https://doi.org/10.1126/science.282.5389.746
Butterworth, B. (2005). The development of arithmetical abilities. Journal of Child Psychology and Psychiatry, 46(1), 3–18. https://doi.org/10.1111/j.1469-7610.2005.00374.x
Chen, F. F. (2007). Sensitivity of goodness of fit indexes to lack of measurement invariance. Structural Equation Modeling: A Multidisciplinary Journal, 14(3), 464-504. https://doi.org/10.1080/10705510701301834
De Smedt, B., & Gilmore, C. K. (2011). Defective number module or impaired access? Numerical magnitude processing in first graders with mathematical difficulties. Journal of experimental child psychology, 108(2), 278-292. https://doi.org/10.1016/j.jecp.2010.09.003
De Smedt, B., Noël, P-L., Gilmore, G., & Ansari, D. (2013). How do symbolic and non-symbolic numerical magnitude processing skills relate to individual differences in children’s mathematical skills? A review of evidence from brain and behavior. Trends in Neuroscience and Education, 2(2), 48–55. https://doi.org/10.1016/j.tine.2013.06.001
Hakkarainen, A., Väisänen, E., Aunio, P., Hellstrand, H., Laakso, M.-J., Laine, A., Räsänen, P., & Korhonen. (2025). Psychometric evidence for the functional numeracy assessment dyscalculia battery (FUNA-DB screener): An online assessment of mathematical learning difficulties. European Journal of Psychological Assessment.
Halberda, J., & Feigenson, L. (2008). Developmental change in the acuity of the ”number sense”: The approximate number system in 3-, 4-, 5-, and 6-year-olds and adults. Developmental Psychology, 44(5), 1457–1465. https://doi.org/10.1037/a0012682
Halberda, J., Ly, R., Wilmer, J. B., Naiman, D. Q., and Germine, L. (2012). Number sense across the lifespan as revealed by a massive internet-based sample. Proc. Natl. Acad. Sci. 109(28), 11116–11120. https://10.1073/pnas.1200196109
Halberda, J., Mazzocco, M. M., & Feigenson, L. (2008). Individual differences in non-verbal number acuity correlate with maths achievement. Nature, 455(7213), 665–668. https://doi.org/10.1038/nature07246
Hays, R. D., & Revicki, D. (2005). Reliability and validity (including responsiveness). Teoksessa P. Fayers & R. Hays (Eds.), Assessing quality of life in clinical trials: Methods and practice (2nd ed., pp. 25–29). Oxford University Press.
Hellstrand, H., Holopainen, S., Korhonen, J., Räsänen, P., Hakkarainen, A., Laakso, M., Laine, A., & Aunio, P. (2024). Arithmetic fluency and number processing skills in identifying students with mathematical learning disabilities. Research in Developmental Disabilities, 151, 104795. https://doi.org/10.1016/j.ridd.2024.104795
Häyrinen, T., Serenius-Sirve, S., & Korkman, M. (2013). Lukilasse-2. Hogrefe Psykologien Kustannus Oy, Helsinki.
Ikäheimo, H. (2011). Kymppikartoitus. Opperi, Helsinki.
Ikäheimo, H. (2011). ALVA-ammattilaislaskennan valmiuksien kartoitus. Opperi, Helsinki.
Ikäheimo, H., Putkonen, H., & Voutilainen, E. (1988). MAKEKO. Matematiikan keskeisen oppiaineksen kokeet luokille 1–9. Opperi.
Ikäheimo, H., Putkonen, H., & Voutilainen E. (N.d.). MaKeKo 1 – 9 Kompassi-digikokeet- Matematiikan keskeisten asioiden kokeet. SanomaPro.
Jordan, N. C., & Hanich, L. B. (2003). Characteristics of children with moderate mathematics deficiencies: A longitudinal perspective. Learning Disabilities Research & Practice, 18(4), 213-221. https://doi.org/10.1111/1540-5826.00076
Jordan, N. C., Kaplan, D., Ramineni, C., and Locuniak, M. N. (2009). Early math matters: Kindergarten number competence and later mathematics outcomes. Develop. Psychol. 45(3), 850–867. http://dx.doi.org/10.1037/a0014939
Kajamies, A. Vauras, M. Kinnunen, R. & Iiskala, T. (2003). Matte – matematiikan sanallisten tehtävien ratkaisutaidon ja laskutaidon arviointi (3.-5lk). Turun yliopisto, Oppimistutkimuksen keskus.
Kananoja, S. (2006). Taidonportaat. Otava.
Koponen, T., Salminen, J., Aunio, P. & Polet, J. (2011). LukiMat – Oppimisen arviointi: Matematiikan tuen tarpeen tunnistamisen välineet esikouluun. Käyttäjän opas. Saatavissa: http://www.lukimat.fi/lukimat-oppimisen-arviointi/materiaalit/tuen-tarpeen-tunnistaminen/esiopetus/matematiikka/kayttajan-opas
Koponen, T., Salminen, J., Aunio, P. & Polet, J. (2011). LukiMat – Oppimisen arviointi: Matematiikan tuen tarpeen tunnistamisen välineet 1. luokalle. Käyttäjän opas. Saatavissa: http://www.lukimat.fi/lukimat-oppimisen-arviointi/materiaalit/tuen-tarpeen-tunnistaminen/1lk/matematiikka/kayttajan-opas.
Koponen, T., Salminen, J., Aunio, P. & Polet, J. (2011). LukiMat – Oppimisen arviointi: Matematiikan tuen tarpeen tunnistamisen välineet 2. luokalle. Käyttäjän opas. Saatavissa: http://www.lukimat.fi/lukimat-oppimisen-arviointi/materiaalit/tuen-tarpeen-tunnistaminen/2lk/matematiikka/kayttajan-opas
Laakso, M.-J., Kaila, E., & Rajala, T. (2018). ViLLE – collaborative education tool: Designing and utilizing an exercise-based learning environment. Education and Information Technologies, 23, 1655–1676. https://doi.org/10.1007/s10639-017-9659-1
Lampinen, A., Ikäheimo, H., & Dräger, M. (2007). MAVALKA 1 ja 2 – Matematiikan valmiuksien kartoitus. Opperi, Helsinki.
Lee, K., Ng, S., & Bull, R. (2018). Learning and solving algebra word problems: The roles of relational skills, arithmetic, and executive functioning. Developmental Psychology, 54(9), 1758-1772. https://doi.org/10.1037/dev0000561
Li, Y., Zhang, M., Chen, Y., Deng, Z., Zhu, X., and Yan, S. (2018). Children’s non-symbolic and symbolic numerical representations and their associations with mathematical ability. Front. Psychol., 9(1035). https://doi.org/10.3389/fpsyg.2018.01035
Liu, Y., Peng, P., & Yan, X. (2025). Early numeracy and mathematics development: A longitudinal meta-analysis on the predictive nature of early numeracy. Journal of Educational Psychology. Advance online publication. https://doi.org/10.1037/edu0000925
Marsh, H., Hau, K.-T., & Wen Z. (2004). In search of golden rules: Comment on hypothesis-testing approaches to setting cutoff values for fit indexes and dangers in overgeneralizing Hu and Bentler’s (1999) findings. Structural Equation Modeling: A Multidisciplinary Journal, 11(3), 320-341. https://doi.org/10.1207/s15328007sem1103_2
Mazzocco, M. M. M., Devlin, K. T., & McKenney, S. J. (2008). Is it a fact? Timed arithmetic performance of children with mathematical learning disabilities (MLD) varies as a function of how MLD is defined. Developmental Neuropsychology, 33(3), 318-344. https://doi.org/10.1080/87565640801982403
Meade, A. W., Johnson, E. C., & Braddy, P. W. (2008). Power and sensitivity of alternative fit indices in tests of measurement invariance. Journal of Applied Psychology, 93(3), 568–592. https://doi.org/10.1037/0021-9010.93.3.568
Mononen, R., Aunio, P., Väisänen, E., Korhonen, J., & Tapola, A. (2017). Matemaattiset oppimisvaikeudet. PS-kustannus.
Musselwhite, D. J., & Wesolowski, B. C. (2018). Standard error of measurement. Teoksessa B. B. Frey (Ed.), The SAGE encyclopedia of educational research, measurement, and evaluation (Vols. 1-4, pp. 1588-1590). SAGE Publications, Inc. http://dx.doi.org/10.4135/9781506326139.n658
Petrill, S., Logan, J., Hart, S., Vincent, P., Thompson, L., Kovas, Y., & Plomin, R. (2012). Math fluency is etiologically distinct from untimed math performance, decoding fluency, and untimed reading performance: evidence from a twin study. Journal of Learning Disabilities, 45(4), 371–381. https://doi.org/10.1177/0022219411407926
Price, G., Mazzocco, M. M. M., & Ansari, D. (2013). Why mental arithmetic counts: Brain activation during single digit arithmetic predicts high school math scores. Journal of Neuroscience 2, 33(1), 156-163. https://doi.org/10.1523/JNEUROSCI.2936-12.2013
Revelle, W. (2021). psych: Procedures for psychological, psychometric, and personality research. Northwestern University, Evanston, Illinois. R package version 2.1.6. Saatavissa: https://CRAN.R-project.org/package=psych
Robin, X., Turck, N., Hainard, A., Tiberti, N., Lisacek, F., Sanchez, J.-C., & Müller, M. (2011). pROC: An open-source package for R and S+ to analyze and compare ROC curves. BMC Bioinformatics, 12(77). https://doi.org/10.1186/1471-2105-12-77
Räsänen P. (2004). RMAT – Laskutaidon testi 9-12-vuotiaille. Niilo Mäki instituutti.
Räsänen P. (2005). Banuca – Lukukäsitteen ja laskutaidon hallinnan testi. Niilo Mäki instituutti.
Räsänen P. & Leino, L. (2005). KTLT – Laskutaidon testi luokka-asteille 7-9. Niilo Mäki instituutti.
Räsänen, P. (2012). Laskemiskyvyn häiriö eli dyskalkulia. Lääketieteellinen Aikakauskirja Duodecim, 128(11):1168-77b. https://www.duodecimlehti.fi/duo10309
Räsänen, P., Aunio, P., Laine, A., Hakkarainen, A., Väisänen, E., Finell, J., Rajala, T., Laakso, M-J., & Korhonen, J. (2021). Effects of gender on basic numerical and arithmetic skills: Pilot data from third to ninth grade for a large-scale online dyscalculia screener. Front. Educ., 6(683672). https://doi.org/10.3389/feduc.2021.683672
Salonen, P., Lepola, J., Vauras, M., Rauhanummi, T., Lehtinen, E. & Kinnunen, R. (1994). Diagnostiset testit 3. Motivaatio, metakognitio ja matematiikka. Oppimistutkimuksen keskus, Turun yliopisto.
Van Luit, J. E. H., Van de Rijt, B. A. M., & Aunio, P. (2006). Lukukäsitetesti. Helsinki: Psykologien kustannus.
Vasilyeva, M., Laski, E., & Shen, C. (2015). Computational fluency and strategy choice predict individual and cross-national differences in complex arithmetic. Developmental Psychology, 51(10), 1489-1500. https://doi.org/10.1037/dev0000045
Xu, F., & Spelke, E. S. (2000). Large number discrimination in 6-month-old infants. Cognition, 74(1), B1-B11. https://doi.org/10.1016/S0010-0277(99)00066-9
Xu, C., Lafay, A., Douglas, H., Di Lonardo Burr, S., LeFevre, J.-A., Osana, H. P., Skwarchuk, S.-L., Wylie, J., Simms, V., & Maloney, E. A. (2021). The role of mathematical language skills in arithmetic fluency and word-problem solving for first- and second-language learners. Journal of Educational Psychology. Advance online publication. https://doi.org/10.1037/edu0000673
Zhang, X., Räsänen, P., Koponen, T., Aunola, K., Lerkkanen, M. K., & Nurmi, J. E. (2020). Early cognitive precursors of children’s mathematics learning disability and persistent low achievement: A 5‐year longitudinal study. Child development, 91(1), 7-27. https://doi.org/10.1111/cdev.13123
Zhang, X., Räsänen, P., Koponen, T., Aunola, K., Lerkkanen, M. K., and Nurmi, J. E. (2017). Knowing, applying, and reasoning about arithmetic: Roles of domain-general and numerical skills in multiple domains of arithmetic learning. Develop. Psychol. 53(12), 2304–2318. https://doi.org/10.1037/dev0000432
Liite 1: Taulukoita FUNA-DB:n osatestien pisteiden kuvailevista tunnusluvuista
Taulukko 1.1
Koulun kielen, sukupuolen ja luokka-asteen mukaan jaotellut FUNA-DB:n osatestien standardoitujen pisteiden kuvailevat tunnusluvut
Huom. N = 18 405. Ka = keskiarvo; Kh = keskihajonta. Lukukäsitteen osatestien pisteet ovat standardoinnin lisäksi käännettyjä.
Taulukko 1.2
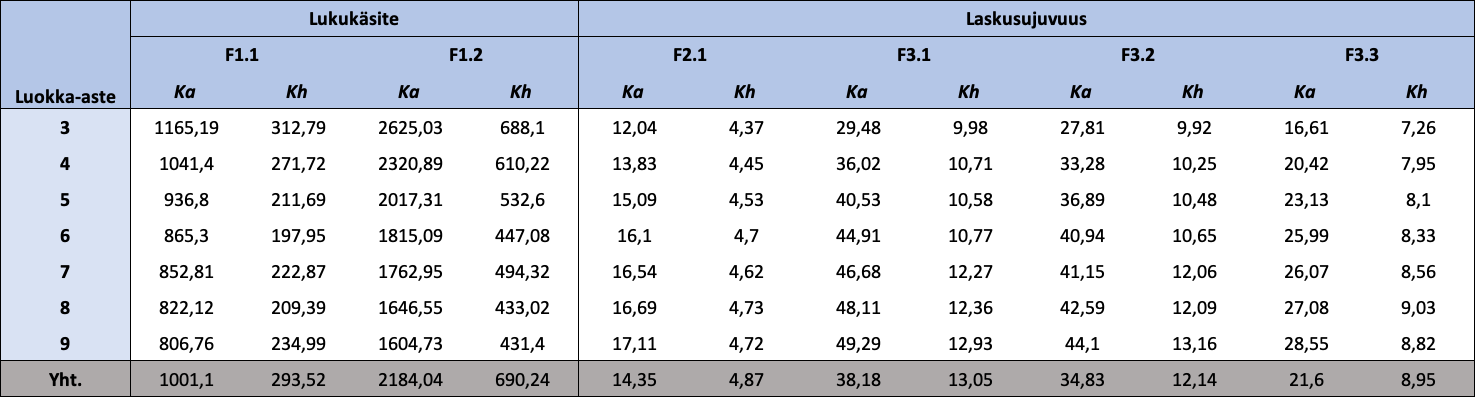
Luokka-asteen mukaan jaotellut FUNA-DB:n osatestien raakapisteiden kuvailevat tunnusluvut
Huom. N = 18 405. Ka = keskiarvo; Kh = keskihajonta. Mitä vähemmän pisteitä Lukukäsitteen osatesteistä, sitä parempi tulos, ja mitä enemmän pisteitä Laskusujuvuuden osatesteistä, sitä parempi tulos. Osatestien pisteiden arvojoukot ([minimi, maksimi]) ovat F1.1: [459,15; 3452,93], F1.2: [415,50; 8102,93], F2.1: [2, 35], F3.1: [2, 80], F3.2: [2, 80] ja F3.3: [2, 57].
Taulukko 1.3
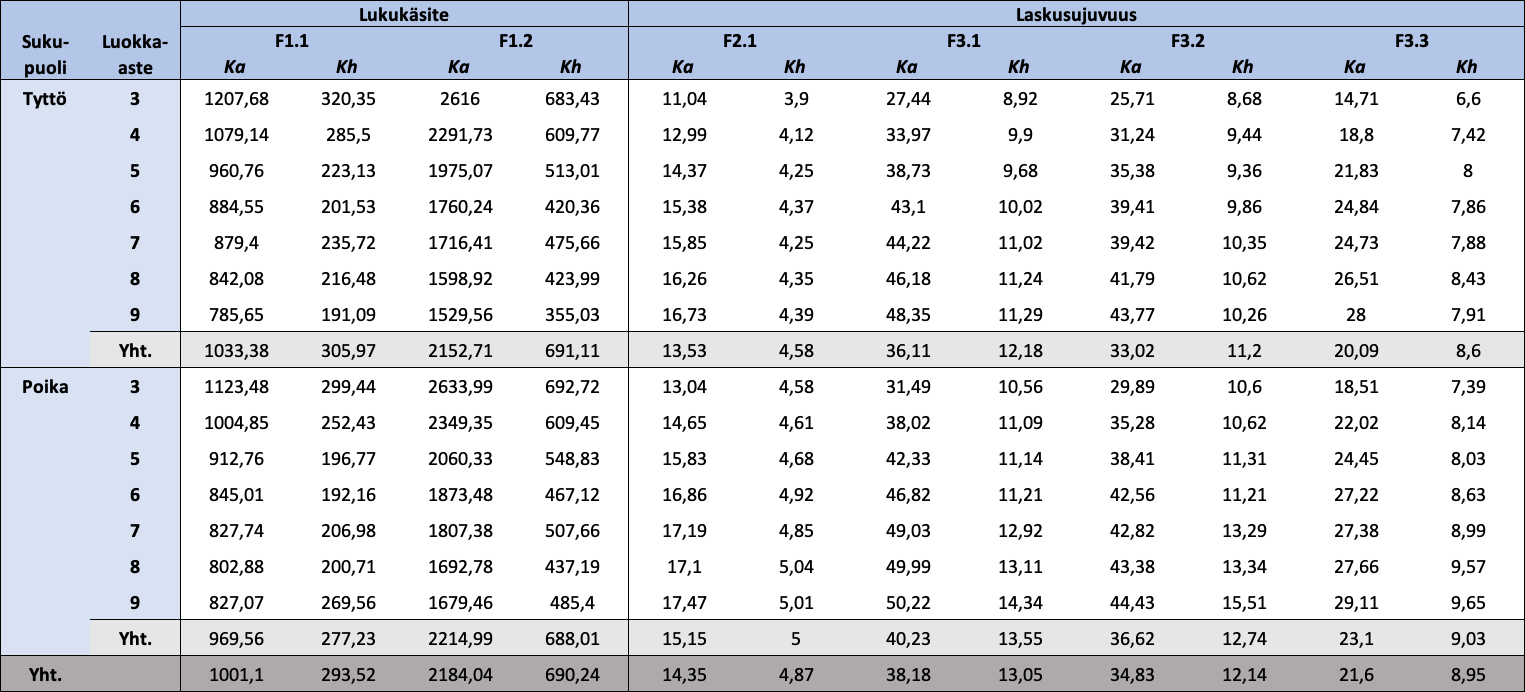
Sukupuolen ja luokka-asteen mukaan jaotellut FUNA-DB:n osatestien raakapisteiden kuvailevat tunnusluvut
Huom. N = 18 405. Ka = keskiarvo; Kh = keskihajonta. Mitä vähemmän pisteitä Lukukäsitteen osatesteistä, sitä parempi tulos, ja mitä enemmän pisteitä Laskusujuvuuden osatesteistä, sitä parempi tulos. Osatestien pisteiden arvojoukot ([minimi, maksimi]) ovat F1.1: [459,15; 3452,93], F1.2: [415,50; 8102,93], F2.1: [2, 35], F3.1: [2, 80], F3.2: [2, 80] ja F3.3: [2, 57].
Taulukko 1.4
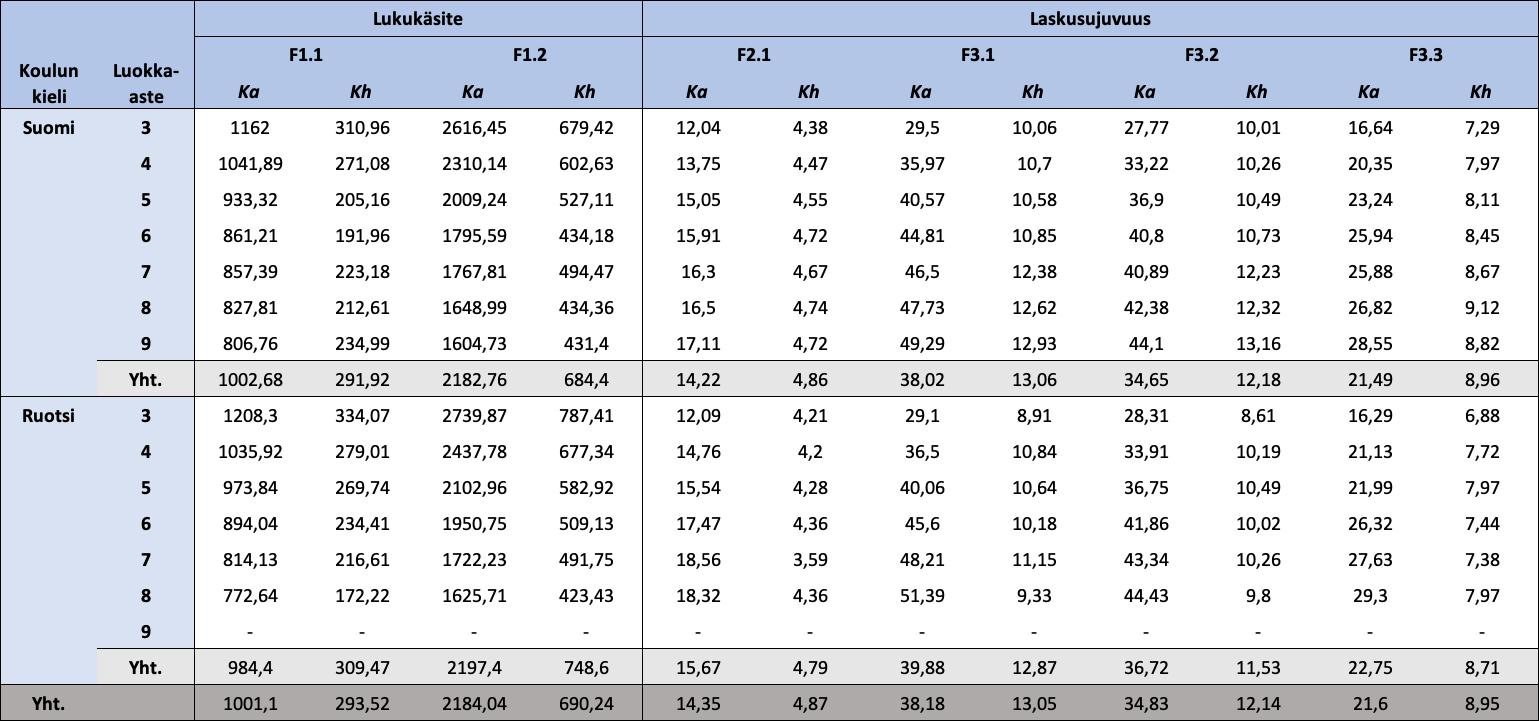
Koulun kielen ja luokka-asteen mukaan jaotellut FUNA-DB:n osatestien raakapisteiden kuvailevat tunnusluvut
Huom. N = 18 405. Ka = keskiarvo; Kh = keskihajonta. Mitä vähemmän pisteitä Lukukäsitteen osatesteistä, sitä parempi tulos, ja mitä enemmän pisteitä Laskusujuvuuden osatesteistä, sitä parempi tulos. Osatestien pisteiden arvojoukot ([minimi, maksimi]) ovat F1.1: [459,15; 3452,93], F1.2: [415,50; 8102,93], F2.1: [2, 35], F3.1: [2, 80], F3.2: [2, 80] ja F3.3: [2, 57].